Matrix Multiplication from foundations

Get Data

import pickle, gzip, os
from pathlib import Path
import json, torch
from itertools import islice
from torch import tensor
import random
from matplotlib import pyplot as plt
from fastcore.test import test_close
from numba import njit
import numpy as np
import math

if 'google.colab' in str(get_ipython()):
  path = Path('fashion_mnist/')
else:
  path = Path('../../data/fashion_mnist/')

os.listdir(path)

['t10k-images-idx3-ubyte.gz',
 'train-labels-idx1-ubyte.gz',
 'train-images-idx3-ubyte.gz',
 't10k-labels-idx1-ubyte.gz']

# taken from https://github.com/zalandoresearch/fashion-mnist/blob/master/utils/mnist_reader.py
def load_mnist(path, kind='train'):
    import os
    import gzip
    import numpy as np

    """Load MNIST data from `path`"""
    labels_path = os.path.join(path,
                               '%s-labels-idx1-ubyte.gz'

    images_path = os.path.join(path,
                               '%s-images-idx3-ubyte.gz'


    with gzip.open(labels_path, 'rb') as lbpath:
        labels = np.frombuffer(lbpath.read(), dtype=np.uint8,
                               offset=8)

    with gzip.open(images_path, 'rb') as imgpath:
        images = np.frombuffer(imgpath.read(), dtype=np.uint8,
                               offset=16).reshape(len(labels), 784)

    return images, labels

class_mapping = [
    "T-shirt/top",
    "Trouser",
    "Pullover",
    "Dress",
    "Coat",
    "Sandal",
    "Shirt",
    "Sneaker",
    "Bag",
    "Ankle boot"
]

X_train, Y_train = load_mnist(path)
X_test, Y_test = load_mnist(path, 't10k')

X_train = X_train / 255.
X_test = X_test / 255.

X_train.dtype

dtype('float64')

X_train.shape, Y_train.shape, X_test.shape, Y_test.shape

((60000, 784), (60000,), (10000, 784), (10000,))

lst1 = list(X_train[0])
vals = lst1[200: 210]
vals

[0.0,
 0.0,
 0.0,
 0.0,
 0.0,
 0.0,
 0.0,
 0.00392156862745098,
 0.0,
 0.27058823529411763]

vals_iter = iter(vals)

next(vals_iter)

0.0

def chunks(lst, sz):
    for i in range(0, len(lst), sz):
        yield lst[i: i + sz]

vals_chunks = chunks(vals, 5)

next(vals_chunks)

[0.0, 0.0, 0.0, 0.0, 0.0]

next(vals_chunks)

[0.0, 0.0, 0.00392156862745098, 0.0, 0.27058823529411763]

plt.imshow(list(chunks(lst1, 28)))

<matplotlib.image.AxesImage>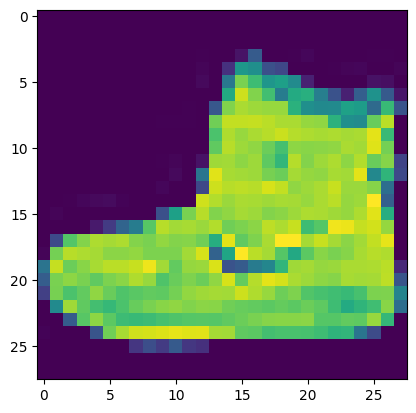

Y_train[0], class_mapping[Y_train[0]]

(9, 'Ankle boot')

vals_iter = iter(vals)

list(islice(vals_iter, 5))

[0.0, 0.0, 0.0, 0.0, 0.0]

it = iter(lst1)

plt.imshow(list(iter(lambda: list(islice(it, 28)), [])))

<matplotlib.image.AxesImage>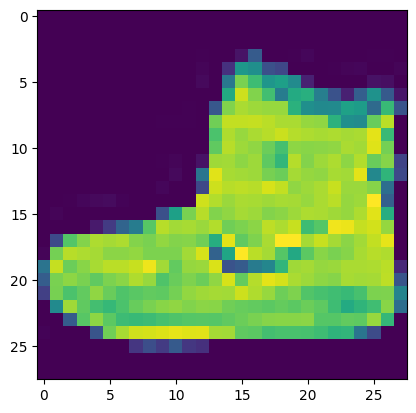

Random Number

rnd_state = None

def seed(x):
    global rnd_state
    x, a = divmod(x, 30326)
    x, b = divmod(x, 30327)
    x, c = divmod(x, 30328)
    rnd_state = int(a) + 1, int(b) + 1, int(c) + 1

def rand():
    global rnd_state
    a, b, c = rnd_state
    x = (172 * a) % 30327
    y = (171 * b) % 30328
    z = (170 * c) % 30329
    rnd_state = x, y, z

    return (x / 30327 + y / 30328 + z / 30329) % 1.0

seed(879828)

rand(), rand(), rand()

(0.3015735034453595, 0.6902815800191595, 0.8979090043518492)

plt.plot([rand() for _ in range(50)])

plt.hist([rand() for _ in range(100_000)])

(array([ 9911., 10047.,  9879.,  9924., 10184.,  9979.,  9943., 10164.,
        10059.,  9910.]),
 array([5.26005285e-06, 1.00004091e-01, 2.00002923e-01, 3.00001754e-01,
        4.00000585e-01, 4.99999417e-01, 5.99998248e-01, 6.99997079e-01,
        7.99995911e-01, 8.99994742e-01, 9.99993573e-01]),
 <BarContainer object of 10 artists>)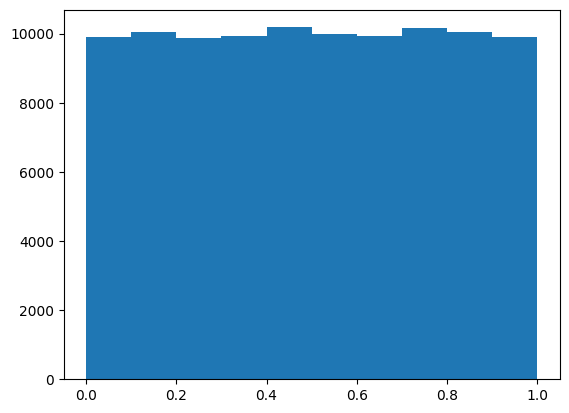

if os.fork(): print(f'In parent {rand()}')
else:
    print(f'In child {rand()}')
    os._exit(os.EX_OK)

In parent 0.9651230962275226

if os.fork(): print(f'In parent {torch.rand(1)}')
else:
    print(f'In child {torch.rand(1)}')
    os._exit(os.EX_OK)

In parent tensor([0.1955])
In child tensor([0.1955])

if os.fork(): print(f'In parent {random.random()}')
else:
    print(f'In child {random.random()}')
    os._exit(os.EX_OK)

In parent 0.1996222936679456
In child 0.5101572296608223

Matrix and Tensor

X_train[100][121]

0.6823529411764706

class Matrix:
    def __init__(self, xs):
        self.xs = xs
    def __getitem__(self, idxs):
        return self.xs[idxs[0]][idxs[1]]

m = Matrix(X_train)

m[100, 121]

0.6823529411764706

imgs = tensor(X_train); imgs[100][121]

tensor(0.6824, dtype=torch.float64)

imgs.dtype

torch.float64

imgs = imgs.reshape(-1, 28, 28)

plt.imshow(imgs[4])

<matplotlib.image.AxesImage>

class_mapping[Y_train[4]]

'T-shirt/top'

5.96 ms ± 2.05 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

134 µs ± 29.1 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Matrix Multiplication

m1 = X_train[:5]; m1

array([[0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.]])

m2 = torch.randn(784, 10); m2.shape

torch.Size([784, 10])

ar, ac = m1.shape
br, bc = m2.shape

c = torch.zeros(ar, bc)

for i in range(ar):
    for j in range(bc):
        for k in range(ac):
            c[i, j] += (m1[i, k] * m2[k, j])

c.shape

torch.Size([5, 10])

def matmul(a, b):
    ar, ac = m1.shape
    br, bc = m2.shape

    c = torch.zeros(ar, bc)

    for i in range(ar):
        for j in range(bc):
            for k in range(ac):
                c[i, j] += (m1[i, k] * m2[k, j])

    return c

t = matmul(m1, m2); t.shape

torch.Size([5, 10])

CPU times: user 989 ms, sys: 2.23 ms, total: 991 ms
Wall time: 997 ms

5*10*784

39200

Matrix Multiplication using numba

@njit
def dot(a, b):
    res = 0
    for i in range(len(a)):
        res += a[i] * b[i]
    return res

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

CPU times: user 440 ms, sys: 153 ms, total: 593 ms
Wall time: 614 ms

32

CPU times: user 10 µs, sys: 2 µs, total: 12 µs
Wall time: 14.8 µs

32

m1[0, :].shape

(784,)

m2[:, 0].shape

torch.Size([784])

def matmul(a, b):
    ar, ac = a.shape
    br, bc = b.shape
    c = torch.zeros(ar, bc)
    for i in range(ar):
        for j in range(bc):
            c[i, j] = dot(a[i,:], b[:, j])
    return c

CPU times: user 87.9 ms, sys: 0 ns, total: 87.9 ms
Wall time: 93.8 ms

test_close(t, matmul(m1, m2.numpy()), eps=1e-4)

Matrix Multiplication using element wise operation

m1 = torch.tensor(m1).float()

m1[0, :].shape, m2[:, 0].shape

(torch.Size([784]), torch.Size([784]))

def matmul(a, b):
    ar, ac = a.shape
    br, bc = b.shape
    c = torch.zeros(ar, bc)
    for i in range(ar):
        for j in range(bc):
            c[i, j] = (a[i, :] * b[:, j]).sum()
    return c

CPU times: user 3.18 ms, sys: 31 µs, total: 3.21 ms
Wall time: 6.33 ms

test_close(t, matmul(m1, m2), eps=1e-4)

def matmul(a, b):
    ar, ac = a.shape
    br, bc = b.shape
    c = torch.zeros(ar, bc)
    for i in range(ar):
        for j in range(bc):
            c[i, j] = torch.dot(a[i, :], b[:, j])
    return c

CPU times: user 2.86 ms, sys: 0 ns, total: 2.86 ms
Wall time: 2.79 ms

test_close(t, matmul(m1, m2), eps=1e-4)

Matrix Multiplication using broadcasting

c = tensor([10, 20, 30]); c

tensor([10, 20, 30])

m = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

t1 = c.expand_as(m); t1.shape

torch.Size([3, 3])

t1.stride(), t1.shape

((0, 1), torch.Size([3, 3]))

t1.storage()

UserWarning: TypedStorage is deprecated. It will be removed in the future and UntypedStorage will be the only storage class. This should only matter to you if you are using storages directly.  To access UntypedStorage directly, use tensor.untyped_storage() instead of tensor.storage()
  t1.storage()

 10
 20
 30
[torch.storage.TypedStorage(dtype=torch.int64, device=cpu) of size 3]

m1

tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]])

m1[0].shape

torch.Size([784])

m1[0, :].shape

torch.Size([784])

m1[0, :, None].shape

torch.Size([784, 1])

m2.shape

torch.Size([784, 10])

(m1[0, :, None] * m2).shape

torch.Size([784, 10])

(m1[0, :, None] * m2).sum(axis=0).shape

torch.Size([10])

def matmul(a, b):
    ar, ac = a.shape
    br, bc = b.shape

    c = torch.zeros(ar, bc)
    for i in range(ar):
        c[i] = (m1[i, :, None] * m2).sum(axis=0)
    return c

test_close(t, matmul(m1, m2), eps=1e-4)

CPU times: user 323 µs, sys: 0 ns, total: 323 µs
Wall time: 330 µs

Using matmul

test_close(t, m1 @ m2, eps=1e-4)

CPU times: user 38 µs, sys: 7 µs, total: 45 µs
Wall time: 48.6 µs

test_close(t, torch.matmul(m1, m2), eps=1e-4)

CPU times: user 43 µs, sys: 0 ns, total: 43 µs
Wall time: 45.8 µs

CPU times: user 28.5 ms, sys: 34.1 ms, total: 62.5 ms
Wall time: 70 ms

CPU times: user 1.31 ms, sys: 0 ns, total: 1.31 ms
Wall time: 2.03 ms

Einstein Summation

m1.shape, m2.shape

(torch.Size([5, 784]), torch.Size([784, 10]))

mr = torch.einsum('ik,kj->ikj', m1, m2); mr.shape

torch.Size([5, 784, 10])

torch.set_printoptions(precision=2, linewidth=14, sci_mode=False)

mr.sum(1)

tensor([[  5.97,
         -26.21,
         -19.14,
          11.53,
          30.43,
           5.51,
         -10.37,
          -3.66,
           6.63,
         -18.34],
        [  4.37,
         -24.84,
         -12.90,
          15.05,
          26.32,
           6.76,
          -5.28,
         -13.98,
          20.55,
         -20.79],
        [ -3.20,
         -10.03,
           0.13,
          11.45,
           6.50,
           1.72,
          -2.58,
           0.95,
           6.77,
          -6.72],
        [ -0.12,
          -1.54,
          -3.97,
          13.97,
          12.62,
          -1.87,
          -3.98,
          -3.59,
           7.12,
          -8.40],
        [-10.83,
         -16.76,
         -12.78,
          10.36,
          24.11,
          15.64,
          -8.89,
           1.78,
           3.56,
         -11.24]])

mr = torch.einsum('ik,kj->ij', m1, m2); mr.shape

torch.Size([5, 10])

test_close(t, mr, eps=1e-4)

CPU times: user 795 µs, sys: 0 ns, total: 795 µs
Wall time: 652 µs

pytorch op

test_close(t, m1@m2, eps=1e-4)

test_close(t, torch.matmul(m1, m2), eps=1e-4)

CPU times: user 39 µs, sys: 7 µs, total: 46 µs
Wall time: 50.1 µs

CUDA

def matmul(grid, a, b, c):
    i, j = grid
    if i < c.shape[0] and j < c.shape[1]:
        temp = 0
        for k in range(a.shape[1]):
            temp += a[i, k] * b[k, j]
        c[i, j] = temp

ar, ac = m1.shape
br, bc = m2.shape
r = torch.zeros(ar, bc)
matmul((0, 0), m1, m2, r)
r

tensor([[5.97,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00],
        [0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00],
        [0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00],
        [0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00],
        [0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00,
         0.00]])

def launch_kernel(kernel, grid_x, grid_y, *args, **kwards):
    for i in range(grid_x):
        for j in range(grid_y):
            kernel((i, j), *args)

grid_x = ar
grid_y = bc
r = torch.zeros(ar, bc)
launch_kernel(matmul, grid_x, grid_y, m1, m2, r)
r

tensor([[  5.97,
         -26.21,
         -19.14,
          11.53,
          30.43,
           5.51,
         -10.37,
          -3.66,
           6.63,
         -18.34],
        [  4.37,
         -24.84,
         -12.90,
          15.05,
          26.32,
           6.76,
          -5.28,
         -13.98,
          20.55,
         -20.79],
        [ -3.20,
         -10.03,
           0.13,
          11.45,
           6.50,
           1.72,
          -2.58,
           0.95,
           6.77,
          -6.72],
        [ -0.12,
          -1.54,
          -3.97,
          13.97,
          12.62,
          -1.87,
          -3.98,
          -3.59,
           7.12,
          -8.40],
        [-10.83,
         -16.76,
         -12.78,
          10.36,
          24.11,
          15.64,
          -8.89,
           1.78,
           3.56,
         -11.24]])

test_close(t, r, eps=1e-4)

from numba import cuda

TPB = 16
rr, rc = r.shape
blockspergrid = (math.ceil(rr / TPB), math.ceil(rc / TPB))

@cuda.jit
def matmul(a, b, c):
  i, j = cuda.grid(2)
  if i < c.shape[0] and j < c.shape[1]:
    tmp = 0.
    for k in range(a.shape[1]):
      tmp += a[i, k] * b[k, j]
    c[i, j] = tmp

r = np.zeros((rr, rc))
m1 = m1.numpy()
m2 = m2.numpy()
m1g, m2g, rg = map(cuda.to_device, (m1, m2, r))

matmul[blockspergrid, (TPB, TPB)](m1, m2, rg)

/usr/local/lib/python3.10/dist-packages/numba/cuda/cudadrv/devicearray.py:886: NumbaPerformanceWarning: Host array used in CUDA kernel will incur copy overhead to/from device.
  warn(NumbaPerformanceWarning(msg))

r = rg.copy_to_host(); r.shape

(5, 10)

test_close(t, r, eps=1e-4)

CPU times: user 3.34 ms, sys: 56 µs, total: 3.4 ms
Wall time: 3.11 ms

m1, m2 = map(torch.tensor, (m1, m2))

CPU times: user 573 µs, sys: 0 ns, total: 573 µs
Wall time: 411 µs