Building makemore - Activations & Gradients, BatchNorm

Imports

#!pip install tqdm

from tqdm import tqdm, tqdm_notebook
import numpy
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plot
import random
import math

g = torch.Generator().manual_seed(42)

Setup

words = open('../data/names.txt', 'r').read().splitlines()
words[:8]

['emma', 'olivia', 'ava', 'isabella', 'sophia', 'charlotte', 'mia', 'amelia']

chars = sorted(list(set(''.join(words))))
stoi = {s: i+1 for i, s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s, i in stoi.items()}

len(words)

32033

def generate_training_set(words, block_size, print_disabled=False):
    
    chars = sorted(list(set(''.join(words))))
    stoi = {s: i+1 for i, s in enumerate(chars)}
    stoi['.'] = 0
    itos = {i:s for s, i in stoi.items()}
    
    X, Y = [], []
    
    for w in words:
        if print_disabled: print(w)
        
        context = [0] * block_size
        for ch in w + '.':
            ix = stoi[ch]
            X.append(context)
            Y.append(ix)
            if print_disabled: print(''.join(itos[i] for i in context), '--->', itos[ix])
            context = context[1:] + [ix] # crop and append
            
    X = torch.tensor(X)
    Y = torch.tensor(Y)
    return X, Y

X, Y = generate_training_set(words, 3)

X.shape, Y.shape

(torch.Size([228146, 3]), torch.Size([228146]))

def generate_train_valid_test_split(words, block_size=3):
    random.seed(42)
    random.shuffle(words)
    n1 = int(0.8*len(words))
    n2 = int(0.9*len(words))

    Xtr, Ytr = generate_training_set(words[:n1], block_size)
    Xdev, Ydev = generate_training_set(words[n1:n2], block_size)
    Xte, Yte = generate_training_set(words[n2:], block_size)
    
    return Xtr, Ytr, Xdev, Ydev, Xte, Yte

Xtr, Ytr, Xdev, Ydev, Xte, Yte = generate_train_valid_test_split(words, block_size=3)

Xtr.shape, Ytr.shape

(torch.Size([182625, 3]), torch.Size([182625]))

Xdev.shape, Ydev.shape

(torch.Size([22655, 3]), torch.Size([22655]))

Xte.shape, Yte.shape

(torch.Size([22866, 3]), torch.Size([22866]))

Train

def compute_logits(parameters, X):
    C, W1, b1, W2, b2 = parameters
    emb = C[X]
    h = torch.tanh(emb.view(-1, W1.shape[0]) @ W1 + b1)
    return h @ W2 + b2

def _regularization_loss(parameters, lambdas):
    return sum(l * (p**2).mean() for p, l in zip(parameters, lambdas))

def initilialize_parameters(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g)
    b1 = torch.randn(hidden_neuron, generator=g)
    W2 = torch.randn((hidden_neuron, 27), generator=g)
    b2 = torch.randn(27, generator=g)
    return [C, W1, b1, W2, b2]

def train(parameters,
          epochs,
          X, 
          Y, 
          bs=32, 
          lambdas = [0, 0, 0],
          enable_print=True,
          print_at_every_nth_epoch=10000
         ):
    
    if not parameters:
        raise Exception("No initial parameters passed")
    
    for p in parameters: p.requires_grad = True 
    
    losses = []
    for epoch in tqdm(range(epochs)):
        
        lr = 0.1 if epoch < 100_000 else 0.01
        
        ix = torch.randint(0, X.shape[0], (bs, ))
        batch_x, batch_y = X[ix], Y[ix]
        logits = compute_logits(parameters, batch_x)
        loss = F.cross_entropy(logits, batch_y)
        regularization_loss = _regularization_loss(parameters, lambdas)
        loss += regularization_loss

        for p in parameters:
            p.grad= None
        loss.backward()


        for p in parameters:
            p.data += - lr * p.grad

        if enable_print and epoch % print_at_every_nth_epoch == 0: print(epoch, loss.item())
            
        losses.append(loss.item())
        
    if enable_print:  print(epoch, loss.item())   
    return losses

params1 = initilialize_parameters(3, 10, 200)

losses = train(params1, 200_000, Xtr, Ytr)

  0%|                                                                                                                                                                  | 50/200000 [00:00<14:51, 224.22it/s]  5%|████████                                                                                                                                                       | 10086/200000 [00:16<05:14, 602.91it/s] 10%|███████████████▉                                                                                                                                               | 19993/200000 [00:36<06:22, 470.09it/s] 15%|███████████████████████▉                                                                                                                                       | 30086/200000 [00:56<05:16, 536.84it/s] 20%|███████████████████████████████▉                                                                                                                               | 40107/200000 [01:15<04:28, 595.70it/s] 25%|███████████████████████████████████████▊                                                                                                                       | 50117/200000 [01:34<04:09, 601.27it/s] 30%|███████████████████████████████████████████████▊                                                                                                               | 60073/200000 [01:50<03:55, 593.51it/s] 35%|███████████████████████████████████████████████████████▋                                                                                                       | 70114/200000 [02:08<03:43, 581.43it/s] 40%|███████████████████████████████████████████████████████████████▋                                                                                               | 80089/200000 [02:26<03:26, 579.70it/s] 45%|███████████████████████████████████████████████████████████████████████▋                                                                                       | 90115/200000 [02:43<03:00, 607.76it/s] 50%|███████████████████████████████████████████████████████████████████████████████                                                                               | 100092/200000 [03:00<02:46, 598.58it/s] 55%|██████████████████████████████████████████████████████████████████████████████████████▉                                                                       | 110109/200000 [03:16<02:30, 599.05it/s] 60%|██████████████████████████████████████████████████████████████████████████████████████████████▉                                                               | 120106/200000 [03:33<02:08, 619.76it/s] 65%|██████████████████████████████████████████████████████████████████████████████████████████████████████▋                                                       | 130061/200000 [03:53<04:29, 259.66it/s] 70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                                               | 140117/200000 [04:14<01:39, 600.35it/s] 75%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌                                       | 150090/200000 [04:30<01:20, 620.44it/s] 80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                               | 160095/200000 [04:47<01:02, 639.88it/s] 85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                       | 170112/200000 [05:02<00:46, 637.91it/s] 90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎               | 180125/200000 [05:18<00:31, 634.12it/s] 95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏       | 190104/200000 [05:34<00:15, 644.02it/s]100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 200000/200000 [05:50<00:00, 571.05it/s]

0 27.642881393432617
10000 2.6563515663146973
20000 2.4569218158721924
30000 2.4299867153167725
40000 2.2356979846954346
50000 2.222148895263672
60000 1.997029423713684
70000 2.013292074203491
80000 2.4996888637542725
90000 2.8243627548217773
100000 2.815431833267212
110000 2.333662509918213
120000 2.5455234050750732
130000 2.3017194271087646
140000 2.1503050327301025
150000 1.8232505321502686
160000 2.411186456680298
170000 2.52275013923645
180000 2.173576593399048
190000 2.165059804916382
199999 2.3922524452209473

plot.plot(losses)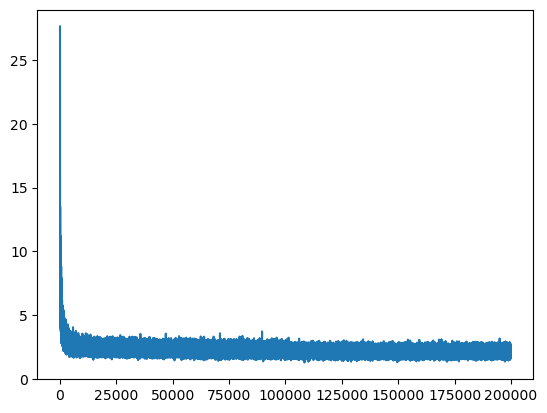

Evaluate Loss

#torch.no_grad()
def evaluate_loss(parameters, X, Y):
    logits = compute_logits(parameters, X)
    return F.cross_entropy(logits, Y)

def loss_split(parameters, dataset='train'):
    dataset_choices = {
        'train': (Xtr, Ytr),
        'valid': (Xdev, Ydev),
        'test': (Xte, Yte)
    }
    return evaluate_loss(parameters, *dataset_choices[dataset])

loss_split(params1), loss_split(params1, 'valid')

(tensor(2.1137, grad_fn=<NllLossBackward0>),
 tensor(2.1547, grad_fn=<NllLossBackward0>))

Sampling

def generate_words(parameters, count, block_size=3):
    for _ in range(count):
        out = []
        context = [0] * block_size # initialize with all ...
        while True:
            logits = compute_logits(parameters, torch.tensor([context]))
            probs = F.softmax(logits, dim=1)
            ix = torch.multinomial(probs, num_samples=1, generator=g).item()
            context = context[1:] + [ix]
            out.append(ix)
            if ix == 0: break

        print(''.join(itos[i] for i in out))

generate_words(params1, 10)

jacklyny.
nita.
sano.
maketissariydah.
jama.
coanley.
zemyni.
khreen.
sis.
cin.

Fixing the initial loss

In the above training, at the 1st epoch the loss is 33.7 then it drops to 2.23

if all the probabilities are uniform then we will expect a loss of

- torch.tensor(1/27.0).log()

tensor(3.2958)

Sample issue

logits = torch.tensor([0.0, 0.0, 0.0, 0.0])
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([0.2500, 0.2500, 0.2500, 0.2500]), tensor(1.3863))

logits = torch.tensor([0.0, 0.0, 5.0, 0.0])
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([0.0066, 0.0066, 0.9802, 0.0066]), tensor(0.0200))

logits = torch.tensor([0.0, 5.0, 0.0, 0.0])
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([0.0066, 0.9802, 0.0066, 0.0066]), tensor(5.0200))

logits = torch.randn(4)
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([0.0808, 0.5283, 0.2293, 0.1616]), tensor(1.4727))

logits = torch.randn(4) * 10
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([1.8579e-01, 8.1123e-01, 1.6882e-04, 2.8133e-03]), tensor(8.6867))

logits = torch.rand(4) 
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([0.3815, 0.2294, 0.2123, 0.1768]), tensor(1.5497))

logits = torch.tensor([1.0, 1.0, 1.0, 1.0])
probs = torch.softmax(logits, dim=0)
loss = -probs[2].log()
probs, loss

(tensor([0.2500, 0.2500, 0.2500, 0.2500]), tensor(1.3863))

params2 = initilialize_parameters(3, 10, 200)

losses = train(params2, 1, Xtr, Ytr)

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00, 357.51it/s]

0 28.708385467529297
0 28.708385467529297

compute_logits(params2, Xtr)[0] # the logits are not uniform

tensor([  9.6100,   0.7546,  -4.9247,  -7.5269, -27.5197,  -7.1780,  -9.5191,
         -6.9432, -11.4050,  15.3572,   3.7384,  24.8570,   5.2003,  -9.1091,
          8.3202,   2.2977,  13.8022,   8.5462, -10.4909,  15.6155,  10.7404,
        -10.5370,   4.4306,  22.4479,  21.0907,  13.4340,   5.8010],
       grad_fn=<SelectBackward0>)

def initilialize_parameters_v2(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g)
    b1 = torch.randn(hidden_neuron, generator=g)
    W2 = torch.randn((hidden_neuron, 27), generator=g) * 0.01
    b2 = torch.randn(27, generator=g) * 0
    return [C, W1, b1, W2, b2]

params3 = initilialize_parameters_v2(3, 10, 200)

losses = train(params3, 1, Xtr, Ytr)

100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00, 66.04it/s]

0 3.2968194484710693
0 3.2968194484710693

compute_logits(params3, Xtr)[0]

tensor([-0.1350,  0.2579, -0.1748,  0.3775, -0.1732, -0.2264, -0.0493, -0.3319,
         0.0467, -0.0121, -0.0923, -0.3330, -0.0462,  0.5159,  0.3215,  0.0554,
        -0.0875, -0.2089, -0.1959,  0.1785,  0.1165, -0.2548, -0.2711, -0.1847,
        -0.3341,  0.3078, -0.2509], grad_fn=<SelectBackward0>)

The logits are closer to zero now

params4 = initilialize_parameters_v2(3, 10, 200)

losses = train(params4, 200_000, Xtr, Ytr)

  0%|                                                                                                                                                                  | 23/200000 [00:00<14:34, 228.75it/s]  5%|████████                                                                                                                                                       | 10114/200000 [00:18<05:16, 599.28it/s] 10%|███████████████▉                                                                                                                                               | 20079/200000 [00:37<05:10, 579.29it/s] 15%|███████████████████████▉                                                                                                                                       | 30114/200000 [00:55<04:55, 575.28it/s] 20%|███████████████████████████████▉                                                                                                                               | 40108/200000 [01:13<04:50, 550.33it/s] 25%|███████████████████████████████████████▊                                                                                                                       | 50088/200000 [01:30<04:06, 607.78it/s] 30%|███████████████████████████████████████████████▊                                                                                                               | 60080/200000 [01:47<03:51, 604.43it/s] 35%|███████████████████████████████████████████████████████▋                                                                                                       | 70121/200000 [02:03<03:34, 604.67it/s] 40%|███████████████████████████████████████████████████████████████▋                                                                                               | 80125/200000 [02:19<03:10, 629.99it/s] 45%|███████████████████████████████████████████████████████████████████████▌                                                                                       | 90074/200000 [02:36<03:05, 591.36it/s] 50%|███████████████████████████████████████████████████████████████████████████████                                                                               | 100078/200000 [02:52<02:44, 608.54it/s] 55%|██████████████████████████████████████████████████████████████████████████████████████▉                                                                       | 110082/200000 [03:08<02:24, 624.28it/s] 60%|██████████████████████████████████████████████████████████████████████████████████████████████▉                                                               | 120123/200000 [03:25<02:08, 622.65it/s] 65%|██████████████████████████████████████████████████████████████████████████████████████████████████████▊                                                       | 130079/200000 [03:42<02:21, 495.27it/s] 70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                                               | 140100/200000 [03:58<01:34, 632.41it/s] 75%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌                                       | 150100/200000 [04:15<01:24, 593.63it/s] 80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                               | 160112/200000 [04:32<01:12, 552.32it/s] 85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                       | 170099/200000 [04:49<00:50, 588.99it/s] 90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎               | 180120/200000 [05:05<00:32, 618.06it/s] 95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏       | 190054/200000 [05:22<00:17, 554.68it/s]100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 200000/200000 [05:39<00:00, 589.22it/s]

0 3.3012616634368896
10000 2.0390188694000244
20000 2.519038200378418
30000 1.9892827272415161
40000 1.973912239074707
50000 2.0713963508605957
60000 1.9657005071640015
70000 2.3061559200286865
80000 1.693084478378296
90000 2.190971851348877
100000 2.581700563430786
110000 1.8936327695846558
120000 2.3227176666259766
130000 1.8893438577651978
140000 2.0941903591156006
150000 2.1335291862487793
160000 2.551553964614868
170000 1.945476770401001
180000 2.069230318069458
190000 1.791576862335205
199999 2.231049060821533

loss_split(params4, 'train'), loss_split(params4, 'valid')

(tensor(2.0690, grad_fn=<NllLossBackward0>),
 tensor(2.1281, grad_fn=<NllLossBackward0>))

Fix the saturated tanh

Plot tanh

x = torch.linspace(-10, 10, 1000)

plot.plot(x, torch.tanh(x))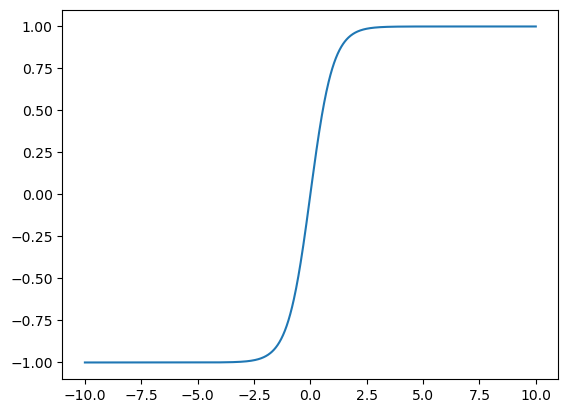

Visualize h

h is the output of tanh in the above neural network

def compute_h(parameters, X):
    C, W1, b1, W2, b2 = parameters
    emb = C[X]
    return torch.tanh(emb.view(-1, W1.shape[0]) @ W1 + b1)

batch_x = Xtr[torch.randint(0, Xtr.shape[0], (32, ))]

h = compute_h(params4, batch_x)

h

tensor([[ 1.0000, -1.0000,  0.2621,  ..., -0.9742,  0.9999, -1.0000],
        [ 1.0000, -1.0000,  0.9999,  ...,  0.2515,  0.1090, -0.8337],
        [ 1.0000, -1.0000,  0.6779,  ..., -0.8491, -0.9900,  0.9737],
        ...,
        [ 0.9999,  0.9009, -0.9950,  ..., -1.0000,  0.9464,  0.9997],
        [ 1.0000,  1.0000, -0.9781,  ...,  0.9608,  0.9965,  0.9994],
        [-0.9998,  0.8074, -0.9989,  ...,  1.0000,  0.9892,  0.9999]],
       grad_fn=<TanhBackward0>)

h.shape

torch.Size([32, 200])

h.view(-1).shape

torch.Size([6400])

plot.hist(h.view(-1).tolist(), 50);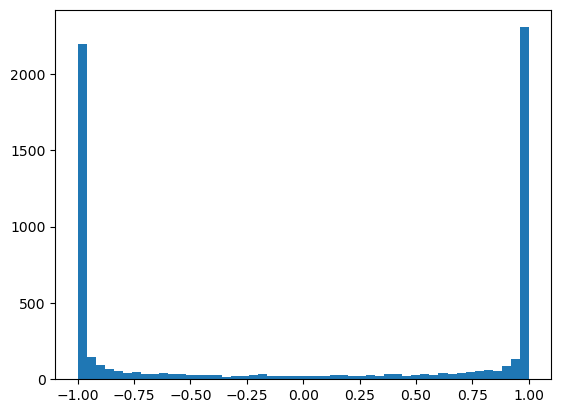

As we can see most values are -1 and 1

def compute_pre_activation(parameters, X):
    C, W1, b1, W2, b2 = parameters
    emb = C[X]
    return emb.view(-1, W1.shape[0]) @ W1 + b1

h_pre_act = compute_pre_activation(params4, batch_x)

plot.hist(h_pre_act.view(-1).tolist(), 50);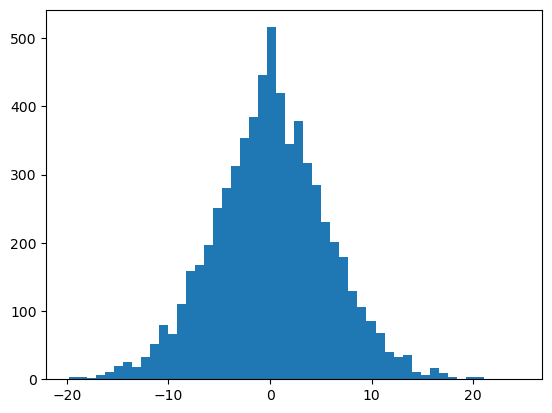

plot.figure(figsize=(20, 10))
plot.imshow(h.abs() > 0.99, cmap='gray', interpolation='nearest')

<matplotlib.image.AxesImage>

The white portion are the ones satisfying h.abs() > 0.99 and black are the ones which are not satisfying the same

As we can see there are lots of whites, and the activations are lying mostly in the region of squashed

The gradient of tanh is (1 - t**2) * out.grad which will be 0 if tanh is +/-1, so there will be no gradients flowing through the network

If in the above image there is a single column of whites then that neuron will not learn anything for the batch of data

The h_pre_act is too off from zero therefore the activations are mostly -1 and 1. Lets change the parameters contributing to h_pre_act

def initilialize_parameters_v3(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g) * 0.1
    b1 = torch.randn(hidden_neuron, generator=g) * 0.01
    W2 = torch.randn((hidden_neuron, 27), generator=g) * 0.01
    b2 = torch.randn(27, generator=g) * 0
    return [C, W1, b1, W2, b2]

params5 = initilialize_parameters_v3(3, 10, 200)

losses = train(params5, 1, Xtr, Ytr)

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00, 273.58it/s]

0 3.2925052642822266
0 3.2925052642822266

h1 = compute_h(params5, batch_x)
plot.hist(h1.view(-1).tolist(), 50);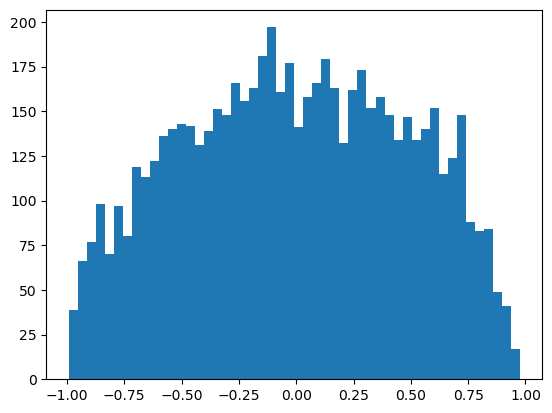

h1_pre_act = compute_pre_activation(params5, batch_x)
plot.hist(h1_pre_act.view(-1).tolist(), 50);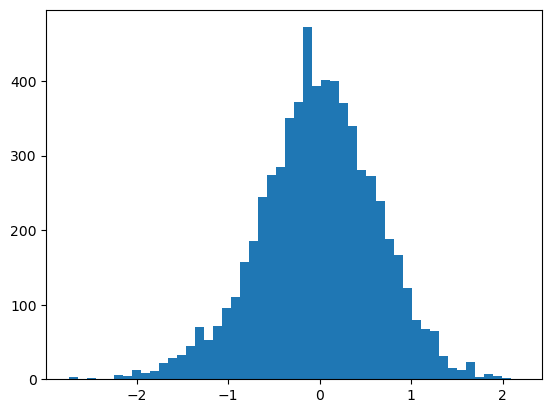

plot.figure(figsize=(20, 10))
plot.imshow(h1.abs() > 0.99, cmap='gray', interpolation='nearest')

<matplotlib.image.AxesImage>

No neurons saturated over 0.99 in either direction

def initilialize_parameters_v4(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g) * 0.2
    b1 = torch.randn(hidden_neuron, generator=g) * 0.01
    W2 = torch.randn((hidden_neuron, 27), generator=g) * 0.01
    b2 = torch.randn(27, generator=g) * 0
    return [C, W1, b1, W2, b2]

params6 = initilialize_parameters_v4(3, 10, 200)

losses = train(params6, 1, Xtr, Ytr)

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00, 387.46it/s]

0 3.315361976623535
0 3.315361976623535

h2 = compute_h(params6, batch_x)
plot.hist(h2.view(-1).tolist(), 50);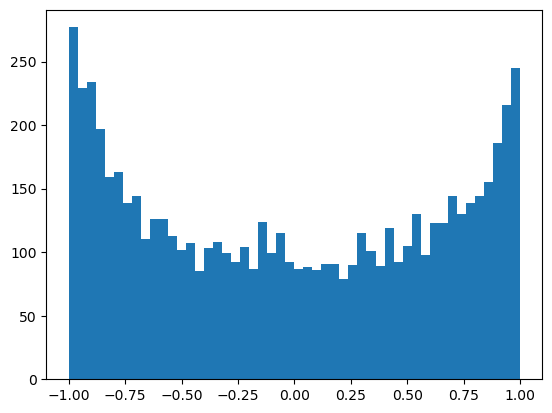

h2_pre_act = compute_pre_activation(params6, batch_x)
plot.hist(h2_pre_act.view(-1).tolist(), 50);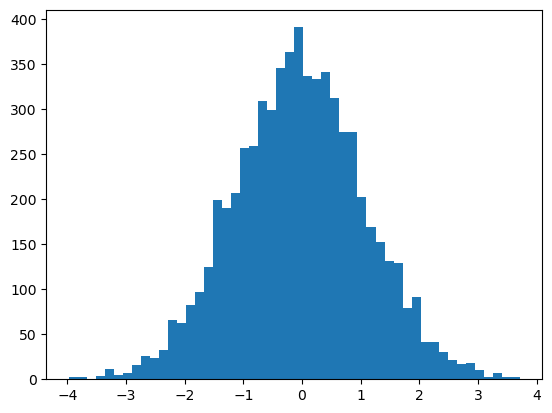

plot.figure(figsize=(20, 10))
plot.imshow(h2.abs() > 0.99, cmap='gray', interpolation='nearest')

<matplotlib.image.AxesImage>

losses = train(params6, 200_000, Xtr, Ytr)

  0%|                                                                                                                                                                 | 114/200000 [00:00<05:52, 566.51it/s]  5%|████████                                                                                                                                                       | 10086/200000 [00:18<05:32, 571.40it/s] 10%|███████████████▉                                                                                                                                               | 20103/200000 [00:37<05:18, 564.13it/s] 15%|███████████████████████▉                                                                                                                                       | 30062/200000 [01:00<07:17, 388.41it/s] 20%|███████████████████████████████▉                                                                                                                               | 40130/200000 [01:20<04:18, 618.81it/s] 25%|███████████████████████████████████████▊                                                                                                                       | 50087/200000 [01:37<04:15, 587.11it/s] 30%|███████████████████████████████████████████████▊                                                                                                               | 60082/200000 [01:54<04:00, 582.39it/s] 35%|███████████████████████████████████████████████████████▋                                                                                                       | 70069/200000 [02:14<05:20, 405.03it/s] 40%|███████████████████████████████████████████████████████████████▋                                                                                               | 80094/200000 [02:38<03:43, 535.66it/s] 45%|███████████████████████████████████████████████████████████████████████▌                                                                                       | 90067/200000 [03:00<03:50, 477.81it/s] 50%|███████████████████████████████████████████████████████████████████████████████                                                                               | 100049/200000 [03:26<03:11, 520.97it/s] 55%|██████████████████████████████████████████████████████████████████████████████████████▉                                                                       | 110095/200000 [03:54<03:16, 457.70it/s] 60%|██████████████████████████████████████████████████████████████████████████████████████████████▊                                                               | 120021/200000 [04:21<02:43, 487.95it/s] 65%|██████████████████████████████████████████████████████████████████████████████████████████████████████▊                                                       | 130064/200000 [04:40<02:11, 531.51it/s] 70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                                               | 140109/200000 [05:01<01:48, 549.81it/s] 75%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌                                       | 150027/200000 [05:22<01:33, 531.64it/s] 80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                               | 160100/200000 [05:45<01:09, 573.43it/s] 85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                       | 170099/200000 [06:03<00:53, 562.53it/s] 90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎               | 180121/200000 [06:22<00:30, 652.22it/s] 95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏       | 190125/200000 [06:38<00:14, 664.52it/s]100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 200000/200000 [16:38:01<00:00,  3.34it/s]

0 3.252462863922119
10000 2.2485759258270264
20000 1.924424648284912
30000 2.3567395210266113
40000 1.7223490476608276
50000 1.9401909112930298
60000 2.2472681999206543
70000 2.110548973083496
80000 1.9843206405639648
90000 2.498479127883911
100000 2.0100741386413574
110000 1.9128767251968384
120000 2.1294615268707275
130000 1.7961547374725342
140000 1.6151217222213745
150000 1.905795693397522
160000 2.0080981254577637
170000 2.0118043422698975
180000 1.73159921169281
190000 2.196617841720581
199999 2.2335524559020996

loss_split(params6, 'train'), loss_split(params6, 'valid')

(tensor(2.0385, grad_fn=<NllLossBackward0>),
 tensor(2.1043, grad_fn=<NllLossBackward0>))

Calculating the init scale: “Kaiming init”

x = torch.randn(1000, 10)
w = torch.randn(10, 200)
y = x @ w
print(x.mean(), x.std())
print(y.mean(), y.std())
plot.figure(figsize=(20, 5))
plot.subplot(121)
plot.hist(x.view(-1).tolist(), 50, density=True);
plot.subplot(122)
plot.hist(y.view(-1).tolist(), 50, density=True);

tensor(-0.0029) tensor(0.9987)
tensor(-0.0028) tensor(3.1829)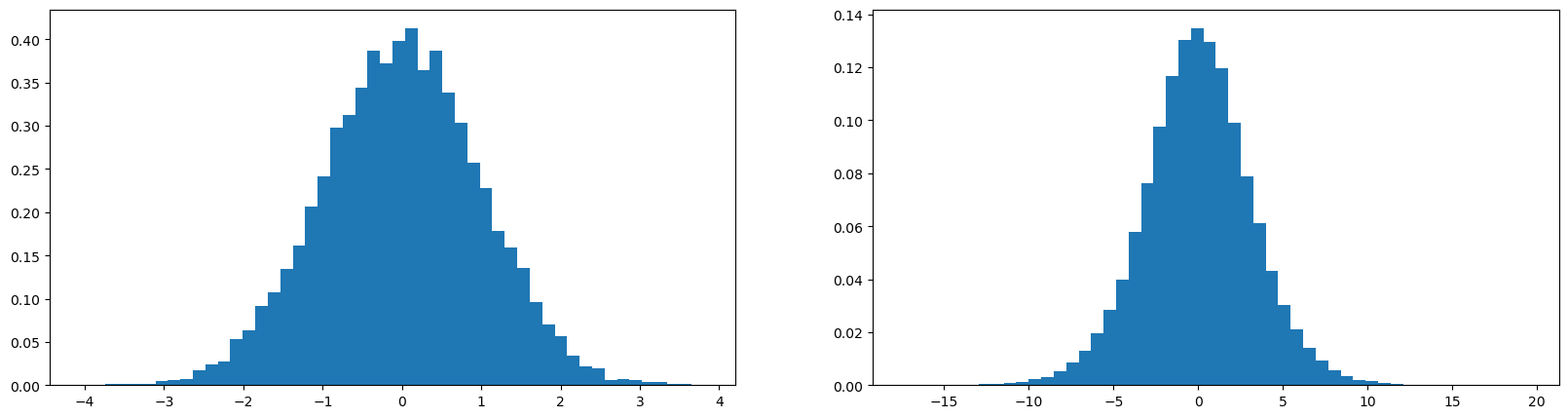

The y has more standard deviation compared to x

The guassian is expanding, we dont want that, we need similar activations during initialization

If we multiply w by a large number i.e. 5, then the standard deviation increases

x = torch.randn(1000, 10)
w = torch.randn(10, 200) * 5
y = x @ w
print(x.mean(), x.std())
print(y.mean(), y.std())
plot.figure(figsize=(20, 5))
plot.subplot(121)
plot.hist(x.view(-1).tolist(), 50, density=True);
plot.subplot(122)
plot.hist(y.view(-1).tolist(), 50, density=True);

tensor(-0.0073) tensor(0.9939)
tensor(0.0191) tensor(15.9527)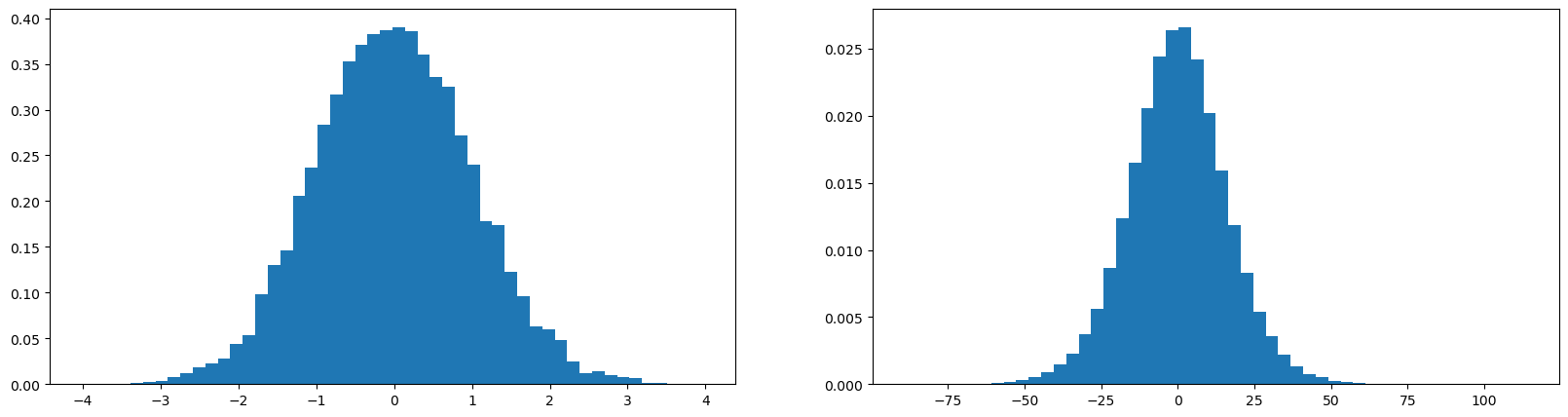

if we multiply w by a small number, then the standard deviation will be smaller

x = torch.randn(1000, 10)
w = torch.randn(10, 200) * 0.2
y = x @ w
print(x.mean(), x.std())
print(y.mean(), y.std())
plot.figure(figsize=(20, 5))
plot.subplot(121)
plot.hist(x.view(-1).tolist(), 50, density=True);
plot.subplot(122)
plot.hist(y.view(-1).tolist(), 50, density=True);

tensor(-0.0038) tensor(0.9879)
tensor(-0.0003) tensor(0.6244)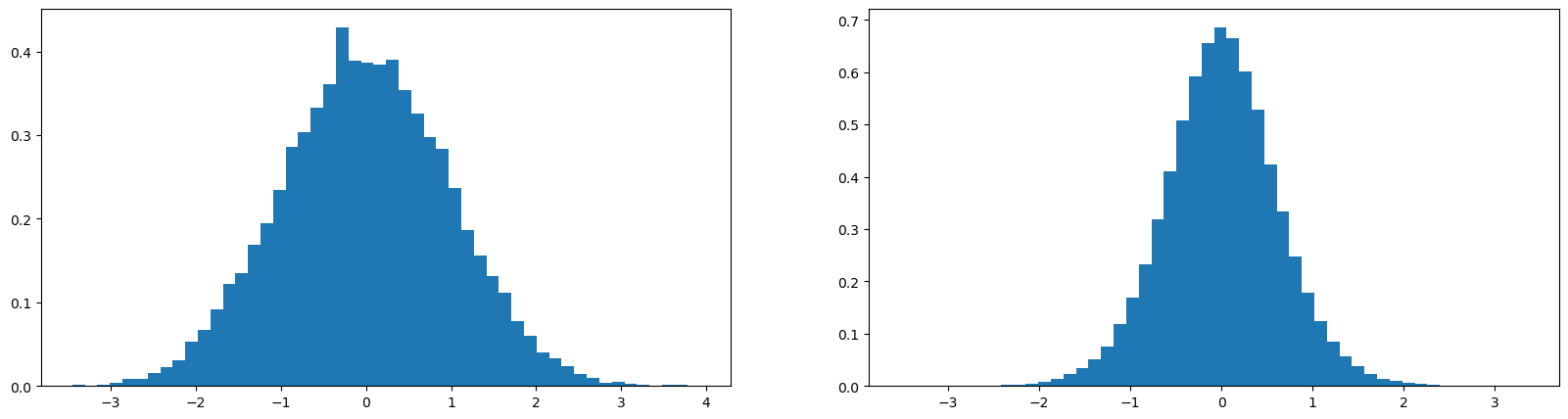

What number should we multiply w by to preserve the standard deviation as 1?

We can multiply by (1/sqrt(fan_in))

x = torch.randn(1000, 10)
w = torch.randn(10, 200) * 1/(math.sqrt(10))
y = x @ w
print(x.mean(), x.std())
print(y.mean(), y.std())
plot.figure(figsize=(20, 5))
plot.subplot(121)
plot.hist(x.view(-1).tolist(), 50, density=True);
plot.subplot(122)
plot.hist(y.view(-1).tolist(), 50, density=True);

tensor(0.0040) tensor(0.9988)
tensor(-0.0010) tensor(0.9846)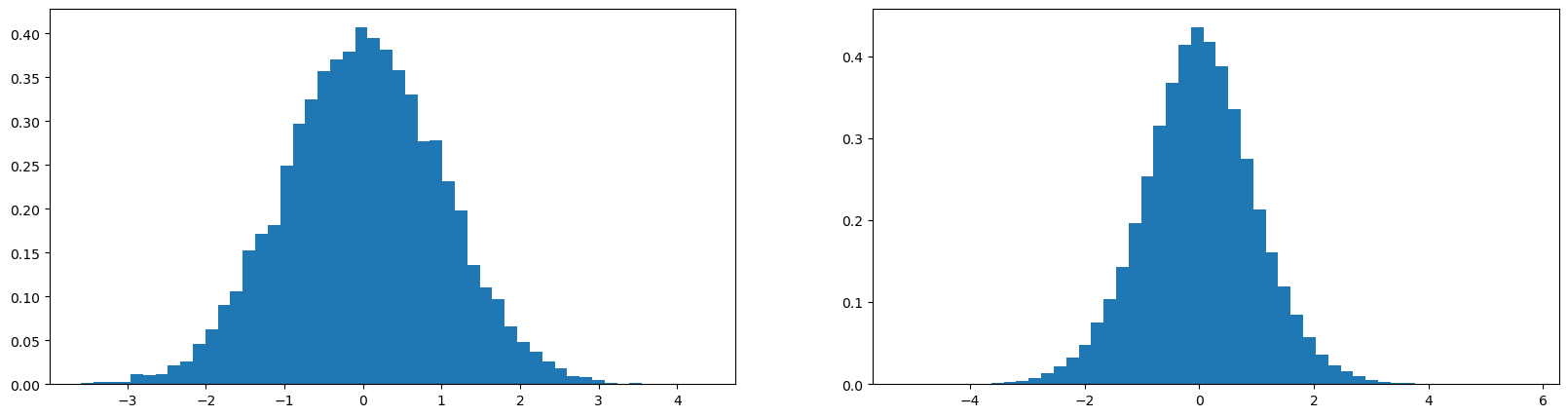

torch.randn(1000)

tensor([-4.4491e-01,  8.1468e-01, -4.9041e-01,  8.5084e-01, -7.5546e-01,
        -1.2834e+00, -1.4080e-01, -1.5628e-01,  7.0759e-01,  5.4389e-01,
         1.0249e+00, -3.6809e-01,  1.5767e-01, -1.2903e-01, -9.6614e-01,
        -5.1882e-01, -1.0040e+00, -9.6146e-01, -4.9114e-02, -1.0125e+00,
         1.0659e+00,  1.3129e+00,  5.9042e-01, -1.3400e-01, -4.0615e-01,
         7.1402e-01,  8.5876e-01,  1.1057e+00, -1.7399e-01, -2.5380e-01,
        -1.9785e-01, -2.2213e+00,  3.8632e-02, -1.4455e+00,  1.4416e+00,
         4.6785e-02,  1.0486e+00,  1.7613e-02,  5.2755e-01, -1.3378e+00,
         7.3152e-01,  1.5148e+00, -9.0945e-01,  9.5265e-01,  1.7500e+00,
        -1.5277e+00, -5.6958e-02, -9.2872e-01, -5.7160e-01, -1.3054e+00,
         2.9642e-01, -9.0971e-01,  1.4852e-01,  4.8295e-01,  2.0170e-02,
        -1.5728e-01,  6.1446e-01, -7.2750e-01,  2.7242e-01, -5.0731e-01,
        -1.6935e+00, -1.1223e+00,  4.0411e-01,  7.8083e-01,  8.9397e-01,
         1.1677e+00, -1.6698e+00, -1.1389e-01, -1.3376e+00, -3.3989e-01,
         4.6134e-01,  1.3889e+00, -2.0328e-01, -8.0168e-01, -1.3011e+00,
         1.7799e-01,  9.1866e-01,  7.4976e-01, -1.7144e+00,  7.3718e-01,
        -3.3846e-01,  1.7048e-01, -1.6116e-01,  5.1980e-01, -3.2220e-01,
         9.6030e-01,  3.0398e-01, -7.1770e-01,  5.1479e-01,  8.8952e-02,
         1.5568e+00, -6.4372e-01, -1.4770e-01, -1.2715e+00,  1.1549e+00,
        -2.2085e+00, -8.0787e-01, -8.0596e-01,  1.1667e+00,  1.1490e+00,
         1.9939e-01,  3.5011e-01,  4.3978e-01,  1.0387e+00,  1.1948e+00,
         6.5371e-01, -1.1983e+00, -7.9712e-02,  9.4302e-01,  7.7875e-01,
        -3.7207e-01,  6.0207e-01,  1.4607e-01,  3.4527e-02, -8.4879e-01,
        -7.7520e-01, -2.9863e-01,  2.2895e-01, -1.8310e+00,  4.8203e-01,
        -1.5591e+00,  1.1811e+00, -6.0453e-01, -3.9585e-01, -1.0402e+00,
         1.1609e+00, -1.3437e+00,  1.3366e+00,  2.7067e+00,  6.6262e-01,
         1.1726e-01, -1.4091e+00,  8.6855e-01, -3.2722e-01, -1.0854e+00,
        -1.7248e-01,  4.2303e-01, -1.0056e-01,  6.7321e-01, -2.1935e-01,
        -1.3298e-01,  3.1146e-01, -3.2207e-01, -8.5663e-01,  1.0111e+00,
        -3.8868e-01,  1.1240e+00,  1.3679e-01, -1.2754e+00,  1.6846e+00,
         1.8569e-01, -1.4316e+00, -5.2817e-01,  4.4829e-01,  1.1192e+00,
        -1.0870e+00,  1.2514e+00,  2.4123e-01,  4.1799e-01,  1.3938e+00,
        -6.4690e-01, -3.2768e-01, -1.0039e+00,  1.0455e+00, -1.1427e+00,
        -3.5521e-01,  3.8842e-01, -1.3270e+00,  1.1490e+00, -1.4166e+00,
        -1.7509e+00, -2.6920e-02, -2.8950e-01,  7.1716e-01, -1.0339e+00,
        -1.4395e-01, -7.5489e-01, -3.2210e-02,  1.3414e+00, -4.4632e-01,
         1.0532e+00, -1.1267e+00,  1.1626e+00, -1.0597e+00,  4.8057e-01,
         1.2193e+00,  9.7095e-01, -4.6855e-01,  9.6808e-01, -7.2747e-01,
        -1.0172e+00, -1.5430e-01, -3.7111e-01,  1.1363e+00,  1.1665e+00,
        -5.7238e-01, -7.2625e-01,  1.1168e+00, -1.9561e+00,  3.6347e-01,
         1.2211e+00, -1.0392e+00,  9.1227e-01, -5.3476e-01,  7.7828e-01,
        -1.8234e-01,  1.2498e+00, -7.6176e-02, -1.4105e-01, -2.7955e-01,
        -7.7375e-01, -2.3475e+00, -7.9845e-01,  8.9417e-01, -4.1188e-01,
         1.1319e+00,  1.2606e-01, -2.1836e+00,  7.5730e-01, -6.8296e-01,
        -1.0518e+00,  1.2614e+00,  3.5788e-01,  3.6420e-01, -3.9252e-01,
        -7.4942e-01, -1.8380e+00,  1.3533e+00, -2.8998e-02, -2.3180e+00,
        -1.9691e-01, -1.2409e+00, -9.2009e-01, -1.9675e-01, -9.7025e-01,
        -1.3910e+00, -6.6132e-01, -1.7533e+00, -1.0233e+00, -2.0021e+00,
        -2.3171e+00, -7.7370e-01, -1.2550e+00,  1.2218e+00,  1.7372e-01,
         8.3574e-01,  1.6951e-01,  1.0796e-01,  1.2036e+00, -1.1552e+00,
         1.7398e-01,  3.1005e-01, -7.4864e-01,  9.1199e-01, -8.1297e-01,
        -1.3774e+00, -4.1376e-02,  1.5385e+00,  1.5433e-01,  7.6850e-01,
        -4.5575e-01, -3.3947e-01,  1.5767e+00, -1.6138e+00,  1.3509e+00,
         7.7009e-01, -1.6286e+00,  1.4196e+00,  8.5499e-01, -6.5572e-01,
         1.0467e+00,  5.3764e-01,  5.4705e-01, -3.0934e-01,  1.4358e+00,
        -2.3142e+00, -2.5676e-01, -6.9334e-01,  6.7920e-01, -1.5806e-02,
         6.6129e-01, -1.1277e-01,  3.7076e-01, -2.0539e+00,  9.6729e-01,
        -1.1464e-01,  9.3331e-02,  7.1655e-01,  2.2155e-01, -2.1334e-01,
        -7.2953e-01, -1.0252e+00,  1.1660e+00,  4.8370e-01, -4.9408e-01,
         8.3829e-01, -8.5957e-01, -6.6706e-02, -6.7575e-01,  9.3957e-01,
         5.0669e-01, -2.3851e-01,  2.9753e-01,  5.4236e-01, -7.0215e-01,
         1.4101e+00,  1.6822e-01,  3.4431e+00,  1.3912e+00, -1.8377e+00,
         1.4642e+00,  5.8495e-01, -8.7159e-01,  1.9798e+00,  4.8268e-01,
         1.1796e+00,  1.8971e+00, -2.2471e-01,  1.4477e+00,  1.4796e+00,
         2.0498e+00,  6.0896e-01,  1.7562e+00, -1.5760e+00, -6.4049e-01,
         1.2525e+00, -1.5839e-01, -8.6765e-01, -6.2326e-01,  1.1278e-01,
        -9.8297e-01, -5.5136e-01,  1.4451e-01,  1.4907e+00, -9.7304e-01,
         1.1056e+00,  1.0133e+00,  6.1220e-01,  4.0848e-01, -6.6162e-01,
        -7.4903e-01,  2.9114e+00,  1.3749e+00, -2.3306e+00, -2.3087e-01,
        -1.1470e+00,  2.0197e+00, -9.6675e-01, -7.4702e-01, -1.0908e-01,
        -2.6147e-01, -3.2547e-01, -1.7522e-01, -2.4414e-01, -3.6424e-01,
        -1.3112e+00, -4.8352e-01, -1.5956e+00, -1.0321e-01,  3.1300e-01,
        -2.2417e-01,  6.4919e-01, -9.9813e-01,  1.9788e+00, -2.3398e+00,
         3.1999e-01,  1.1417e+00, -7.2538e-02,  7.5595e-01, -1.1833e+00,
        -1.0342e+00,  1.3779e+00,  4.6179e-01, -4.4127e-01, -1.5523e+00,
         2.4986e+00, -1.4134e+00,  8.8584e-01,  3.8325e-01,  3.0485e-01,
         1.8157e+00, -7.2691e-01, -4.9207e-01,  8.3230e-01,  1.0072e+00,
        -8.1437e-01, -1.3365e-01,  3.8920e-01, -1.0508e-01, -1.1311e+00,
        -8.0398e-01,  3.3417e-01,  3.9109e-01, -9.8168e-01, -1.1504e+00,
         9.3065e-01, -2.1849e-01, -2.7455e-03,  1.5553e+00, -1.5637e-01,
         1.1848e-01, -9.1837e-01, -1.1483e-01, -5.6455e-01, -6.8401e-02,
         5.4284e-01,  6.9041e-01,  1.5359e+00,  6.5503e-02,  1.2606e+00,
        -2.3238e-01,  5.0018e-01,  4.0842e-01,  1.2282e-01, -8.3332e-01,
        -5.2143e-01,  1.0709e-01,  5.5946e-01, -1.7920e+00,  9.8011e-02,
         2.3607e-01,  9.1122e-01, -1.7815e+00, -2.2378e+00,  6.0846e-01,
        -1.0682e+00,  6.7406e-01,  1.1799e+00, -2.7380e-02,  1.1086e+00,
         1.2985e-01, -1.5836e+00,  9.9837e-01, -8.8163e-01,  4.2766e-01,
        -7.5449e-01, -9.1209e-01,  8.2167e-01, -1.3376e+00, -5.5470e-01,
        -2.5744e+00,  2.3497e+00,  9.1383e-01, -8.6754e-01,  2.6851e-02,
        -5.6935e-01,  1.7634e+00, -5.4466e-01,  6.4427e-01, -2.8968e+00,
         1.0398e+00, -1.7710e+00,  2.6833e-01,  9.7795e-01, -5.1294e-01,
        -4.4039e-01,  8.8880e-01, -1.5962e+00,  2.2802e-01,  9.9065e-01,
        -3.9762e-01, -8.1780e-01,  2.2655e+00, -1.6902e+00, -1.0324e-01,
         1.4844e+00,  5.5991e-01, -1.9720e+00,  2.3696e+00,  1.4115e-01,
        -1.0652e+00, -9.0866e-01,  1.1514e+00,  1.6936e+00,  4.7878e-01,
        -2.9971e-01,  5.4005e-01,  7.3565e-01, -4.4122e-01, -6.8278e-01,
         5.9391e-01, -7.5252e-01, -6.0103e-01, -4.1738e-01, -6.0496e-01,
        -1.9164e+00,  3.4902e-01,  6.5277e-02, -1.8154e-01,  9.1510e-01,
        -9.1029e-02, -2.4382e-01,  2.3432e+00,  1.9859e+00, -7.8514e-01,
         1.2721e-01,  1.4515e+00, -1.2700e-01, -1.6711e-01,  6.6730e-01,
        -1.6903e-01,  1.0743e-01, -1.1094e+00, -1.0274e+00,  3.7128e-01,
        -2.3233e-01, -3.0973e-01,  1.8141e+00,  1.9199e-01, -1.8364e+00,
        -2.1589e-01, -7.8127e-02, -3.4849e-01, -2.1622e+00,  4.0660e-01,
        -9.5050e-01, -9.0194e-01, -5.4401e-01,  1.9922e+00,  5.5333e-01,
         2.2488e-01, -4.8751e-01,  7.1682e-01,  3.6225e-01,  8.9288e-01,
        -8.5990e-01,  9.6229e-01,  9.5417e-01, -5.1965e-01, -2.3035e+00,
        -4.9344e-01, -1.7938e+00,  9.6043e-01,  3.4079e-01, -6.7608e-01,
         1.1257e+00, -2.9176e-01, -2.4500e-01,  2.1111e+00, -9.0706e-01,
         2.4174e+00,  1.8432e+00,  8.5921e-01,  3.7028e-02,  3.3475e-01,
        -1.2499e+00, -2.7984e-01, -9.5921e-02, -1.2070e+00, -5.6210e-01,
        -7.6785e-01, -1.0238e-01, -4.1785e-01, -1.0449e+00,  1.4974e+00,
        -9.2206e-01,  8.6997e-02, -7.2990e-01, -5.8177e-02,  1.2354e+00,
        -1.8226e-02, -1.2640e+00, -8.9501e-01, -1.2832e+00, -4.8085e-01,
         1.0304e+00, -2.2113e+00, -4.8045e-01, -5.8689e-01,  9.0754e-01,
         2.4374e-01, -5.2606e-01, -6.5553e-01, -3.4300e-01,  6.7370e-01,
         9.0023e-01,  1.2187e+00,  1.0026e+00, -5.2062e-01, -1.2393e+00,
        -7.0569e-01,  1.3346e+00, -1.0457e+00, -2.1257e-02, -4.9760e-01,
        -6.0507e-01,  1.4430e+00,  3.0979e-01, -1.2321e+00,  1.8128e-01,
         4.8367e-01,  5.6369e-01, -9.7980e-02,  1.4244e+00,  9.5563e-02,
         8.2211e-01,  1.2565e+00,  1.7145e+00,  1.8543e+00,  8.3598e-01,
        -1.5805e+00,  4.4981e-01,  4.9791e-01,  1.5932e+00, -7.8263e-01,
         1.1016e+00, -1.4328e+00, -1.3174e-01, -2.3278e-01,  1.2399e+00,
        -1.1156e-01, -1.0908e+00, -8.6325e-01, -1.2553e-02, -2.0168e-01,
         9.7023e-02,  6.2413e-01,  4.3617e-01, -7.6339e-01,  1.7359e+00,
        -8.8891e-02,  1.1993e+00,  1.2335e+00, -1.7588e-01, -1.1068e+00,
         1.5370e+00,  5.3286e-01, -1.7069e+00, -7.0883e-01,  6.0098e-01,
        -1.8722e+00,  1.0028e+00, -1.7522e+00,  1.9773e+00,  7.6629e-02,
         9.7794e-01,  9.1844e-01,  3.6816e-02,  7.0968e-01,  1.4424e+00,
        -8.8674e-01,  9.6100e-01,  4.4609e-01, -3.7348e-01,  2.1652e+00,
        -2.0705e-01,  2.8895e+00, -8.2157e-03,  1.0014e-01,  1.3509e+00,
        -9.2852e-01, -1.4189e+00, -3.4976e-01,  1.1974e-01, -6.0752e-01,
         1.2418e+00,  1.4813e+00, -2.9009e-01, -6.5577e-02, -3.7928e-01,
         4.0710e-01, -7.4858e-02,  5.8135e-01,  1.4308e+00,  4.6332e-01,
         1.5282e+00, -1.1648e+00, -1.3339e+00,  8.2611e-01, -8.9988e-02,
         1.2866e+00,  9.7417e-04, -1.0353e+00, -7.7178e-01,  1.5070e+00,
         1.3771e+00, -1.4094e+00,  4.6631e-02,  6.4983e-01,  4.4373e-01,
         4.3267e-01, -1.5054e-01, -7.0889e-01, -4.7002e-01, -1.2221e+00,
         1.1314e-01,  2.0500e-01,  5.8394e-01, -1.1366e-02,  1.1042e-02,
        -5.1476e-01, -1.6741e+00,  1.8323e+00, -3.9113e-01,  3.0786e-01,
         5.6348e-01, -2.2628e-01, -1.0945e+00, -2.5047e+00, -1.3732e-01,
        -9.4335e-01,  9.3365e-01, -1.3367e-01,  5.3266e-01, -7.3486e-01,
        -1.2251e+00,  1.5481e+00,  7.1739e-01,  1.1879e+00,  8.1519e-01,
         2.0114e-01, -1.6691e+00, -2.9070e-02, -1.6126e+00,  2.6002e-01,
         1.7315e+00, -3.7181e-01,  1.7891e+00,  2.6855e-02,  1.3394e+00,
        -1.2826e-01,  6.9187e-01,  5.2593e-01,  5.1028e-01, -2.9707e-01,
         1.0332e+00,  7.6733e-01,  2.4797e+00, -1.6167e-01,  6.6452e-02,
         9.0616e-01,  7.1738e-01,  7.1106e-01,  9.8761e-02, -1.0895e+00,
        -8.7591e-01,  8.7157e-01,  1.9313e+00, -6.2044e-01,  3.4145e-02,
        -3.4549e-01,  5.2566e-01, -6.1216e-01,  4.0845e-01,  1.2780e+00,
        -6.7273e-01, -1.6323e+00,  1.3512e+00,  7.9965e-02,  1.2352e-01,
        -2.9542e-01,  1.5546e+00, -2.2835e-01, -1.1723e+00, -8.9304e-01,
        -9.0590e-01, -3.3402e-01,  5.9588e-01,  1.6975e-01, -1.3846e+00,
         8.1981e-01,  2.4207e-02,  1.1152e-01,  2.1979e+00,  4.7347e-01,
        -3.6197e-02, -7.3026e-03, -6.8270e-01, -8.8449e-01,  3.6973e-01,
         7.1029e-01,  1.6141e-01,  3.9045e-01, -1.6220e-01, -1.0303e-02,
         2.9736e-01, -2.5634e-01, -7.6549e-01,  7.0336e-01,  4.5149e-01,
        -3.2849e-01, -1.6511e+00,  6.9789e-01,  1.1553e+00, -1.5515e+00,
         1.1479e+00,  7.9370e-01, -1.1824e+00, -8.7946e-01,  1.3841e+00,
        -1.8442e+00,  9.5913e-01, -1.0785e+00,  2.8138e-01,  1.4519e+00,
         1.6403e+00, -1.6989e+00, -1.7778e+00, -1.3598e+00, -6.3483e-01,
         5.2751e-01,  4.9287e-01,  5.0181e-01, -6.0085e-01,  6.2637e-01,
        -7.0738e-01,  4.8160e-01, -1.1089e-01,  7.4083e-01, -8.9509e-01,
         9.0353e-01, -4.0467e-01, -8.5919e-02,  2.6746e-01, -1.9548e+00,
         6.0947e-01,  8.7655e-01, -6.5896e-01, -6.1613e-01,  1.7297e+00,
         1.9492e-01, -1.8195e+00,  2.2503e-02, -1.9076e+00,  7.5093e-02,
         1.6529e+00,  3.4259e-01,  1.4164e+00,  1.5928e+00, -4.3144e-01,
        -9.2303e-01, -4.6064e-01, -4.6902e-01, -1.5084e+00,  8.9347e-01,
         1.1865e+00, -9.3348e-01,  8.6712e-01, -3.0535e-01, -7.8115e-01,
         1.8942e+00,  4.7689e-01,  6.3666e-01, -2.2987e-01,  2.2629e+00,
        -3.9918e-01, -1.7252e+00,  1.5192e+00, -2.2920e+00,  2.6366e-01,
        -6.8147e-02,  1.3599e-01,  1.3921e+00,  1.6916e-01,  1.2853e+00,
        -1.9718e+00, -5.3289e-01,  1.2188e+00, -2.4011e-01, -4.4860e-01,
        -5.3689e-01, -5.2381e-01,  1.0976e-01,  5.2891e-01, -9.0536e-01,
        -5.3731e-01, -5.0766e-01, -1.2572e+00, -1.3832e+00,  1.0783e+00,
        -5.6167e-01,  3.8724e-01,  1.8097e-01, -5.9655e-01, -9.2021e-01,
        -2.1552e+00,  1.3431e-01, -1.2162e+00, -1.5789e+00, -4.1252e-01,
        -1.0802e+00, -6.0434e-02, -3.3154e-01,  1.1832e+00,  7.1232e-01,
        -1.1653e+00, -2.1207e+00,  2.2294e-01, -4.0428e-01,  1.6746e+00,
        -9.8364e-01, -1.8898e+00,  4.7501e-02, -1.9037e-02,  6.3712e-01,
        -5.2208e-01,  1.1077e+00,  5.4200e-02,  4.3732e-01,  9.7521e-01,
         4.4448e-01,  8.5956e-01,  5.4088e-01, -7.5151e-01, -8.2385e-02,
         2.7066e+00, -4.0313e-01, -1.2705e+00, -1.8110e-03, -7.9295e-01,
        -4.0852e-01, -7.5687e-01,  1.1580e+00,  3.5440e-01,  8.5731e-01,
        -1.4712e+00,  1.6121e-01, -4.4616e-01,  2.1555e+00,  6.6903e-02,
        -1.2607e+00, -2.2889e-01, -2.4372e-02,  1.6145e+00,  1.6716e+00,
         4.4838e-01, -1.8342e-01,  7.2343e-01, -1.0761e+00,  2.1152e+00,
        -1.0926e+00,  7.0204e-01, -3.3275e-01,  2.6774e-02, -3.8973e-01,
        -1.2466e+00,  5.2782e-01, -5.4509e-01,  4.6797e-01,  9.5262e-01,
         3.0096e-02, -1.1982e+00, -6.1488e-01,  5.2910e-01, -4.2660e-01,
        -1.1221e+00, -3.5857e-01,  2.8266e-01, -6.7295e-01, -6.9349e-01,
         8.0775e-01,  5.0606e-01,  1.9053e+00,  1.2228e+00,  4.7014e-01,
         3.8042e-01, -5.3530e-01, -1.6741e-01,  1.2887e+00, -1.3320e+00,
         1.2936e+00,  1.0690e+00,  1.3661e+00,  6.7960e-01, -4.4733e-01,
         6.9975e-01,  1.8949e-01,  3.4809e-02, -1.2910e-01,  1.0193e+00,
        -1.7590e-01, -2.5930e-01,  3.2330e-01, -2.9028e-01, -5.4029e-01,
        -8.1340e-01, -1.1686e+00,  9.4940e-01, -6.8079e-02, -3.1358e-01,
        -2.6569e-01, -3.5748e-01,  1.4510e+00, -7.5871e-01,  9.6715e-01,
         3.7772e-01,  8.1767e-01, -1.7959e+00, -3.8471e-01, -1.3908e+00,
        -7.9921e-01, -1.6201e+00, -1.7005e-01,  9.1469e-01,  1.7542e+00,
        -1.3094e+00, -1.0830e+00, -2.7837e+00,  3.6276e-01,  3.3478e-01])

(torch.randn(1000) * 0.2).std()

tensor(0.2046)

std_dev = (5/3) / (30 ** 0.5); std_dev

0.3042903097250923

def initilialize_parameters_v5(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g) * ((5/3) / ((embedding_size * block_size) ** 0.5))
    b1 = torch.randn(hidden_neuron, generator=g) * 0.01
    W2 = torch.randn((hidden_neuron, 27), generator=g) * 0.01
    b2 = torch.randn(27, generator=g) * 0
    return [C, W1, b1, W2, b2]

params7 = initilialize_parameters_v5(3, 10, 200)

losses = train(params7, 200_000, Xtr, Ytr)

  0%|                                                                                                                                                                 | 132/200000 [00:00<05:09, 645.01it/s]  5%|████████                                                                                                                                                       | 10125/200000 [00:14<04:19, 733.07it/s] 10%|███████████████▊                                                                                                                                             | 20084/200000 [1:00:00<04:29, 668.33it/s] 15%|███████████████████████▋                                                                                                                                     | 30138/200000 [1:00:14<04:01, 702.35it/s] 19%|██████████████████████████████▌                                                                                                                              | 38883/200000 [4:01:38<04:25, 605.88it/s] 25%|███████████████████████████████████████▎                                                                                                                     | 50091/200000 [4:01:54<03:29, 715.16it/s] 30%|███████████████████████████████████████████████▏                                                                                                             | 60084/200000 [4:02:09<03:31, 661.46it/s] 35%|███████████████████████████████████████████████████████                                                                                                      | 70071/200000 [4:02:24<03:19, 650.30it/s] 40%|██████████████████████████████████████████████████████████████▉                                                                                              | 80121/200000 [4:02:39<02:59, 667.73it/s] 45%|██████████████████████████████████████████████████████████████████████▋                                                                                      | 90110/200000 [4:02:55<02:37, 695.86it/s] 50%|██████████████████████████████████████████████████████████████████████████████                                                                              | 100130/200000 [4:03:10<02:26, 680.25it/s] 55%|█████████████████████████████████████████████████████████████████████████████████████▊                                                                      | 110085/200000 [4:03:25<02:17, 655.44it/s] 60%|█████████████████████████████████████████████████████████████████████████████████████████████▋                                                              | 120089/200000 [4:03:40<02:04, 644.20it/s] 65%|█████████████████████████████████████████████████████████████████████████████████████████████████████▍                                                      | 130067/200000 [4:03:55<01:46, 655.76it/s] 70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▏                                              | 140063/200000 [4:04:10<01:29, 666.43it/s] 75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████                                       | 150093/200000 [4:04:25<01:19, 628.04it/s] 80%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉                               | 160115/200000 [4:04:40<00:53, 743.59it/s] 85%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                       | 170077/200000 [4:04:54<00:44, 677.63it/s] 90%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍               | 180117/200000 [4:05:08<00:26, 751.15it/s] 95%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎       | 190117/200000 [4:05:23<00:14, 702.81it/s]100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 200000/200000 [4:05:37<00:00, 13.57it/s]

0 3.2795920372009277
10000 2.470160484313965
20000 2.183413505554199
30000 2.3951308727264404
40000 1.8953704833984375
50000 2.1281423568725586
60000 2.08463454246521
70000 1.564221739768982
80000 2.0972611904144287
90000 2.21366810798645
100000 2.302164077758789
110000 1.839044451713562
120000 1.8937313556671143
130000 2.7189743518829346
140000 2.1313252449035645
150000 1.9625704288482666
160000 1.89139723777771
170000 1.889981985092163
180000 1.9499194622039795
190000 1.9968667030334473
199999 1.9478144645690918

loss_split(params7, 'train'), loss_split(params7, 'valid')

(tensor(2.0388, grad_fn=<NllLossBackward0>),
 tensor(2.1015, grad_fn=<NllLossBackward0>))

Batch Normalization

Normalization

h_pre_act = compute_pre_activation(params7, batch_x)
h_pre_act.shape

torch.Size([32, 200])

h_pre_act_mean = h_pre_act.mean(0, keepdim = True)
h_pre_act_mean.shape

torch.Size([1, 200])

h_pre_act_std = h_pre_act.std(0, keepdim = True)
h_pre_act_std.shape

torch.Size([1, 200])

h_pre_act_norm = (h_pre_act - h_pre_act_mean)/h_pre_act_std
h_pre_act_norm.shape

torch.Size([32, 200])

Define new training

def initilialize_parameters_v6(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g) * ((5/3) / ((embedding_size * block_size) ** 0.5))
    b1 = torch.randn(hidden_neuron, generator=g) * 0.01
    W2 = torch.randn((hidden_neuron, 27), generator=g) * 0.01
    b2 = torch.randn(27, generator=g) * 0
    
    bngain = torch.ones((1, hidden_neuron)) # for scale in batch normalization
    bnbias = torch.zeros((1, hidden_neuron)) # for shift in batch normalization
    
    return [C, W1, b1, W2, b2, bngain, bnbias]

def compute_logits_v2(parameters, X):
    C, W1, b1, W2, b2, bngain, bnbias = parameters
    emb = C[X]
    embcat = emb.view(-1, W1.shape[0]) 
    h_pre_act = embcat @ W1 + b1
    h_pre_act_norm = (h_pre_act - h_pre_act.mean(0, keepdim = True)) / h_pre_act.std(0, keepdim = True)
    h_pre_act_scale_shift = bngain * h_pre_act_norm + bnbias
    h = torch.tanh(h_pre_act_scale_shift)
    logits = h @ W2 + b2
    return logits

def train_v2(parameters,
          epochs,
          X, 
          Y, 
          bs=32, 
          lambdas = [0, 0, 0],
          enable_print=True,
          print_at_every_nth_epoch=10000
         ):
    
    if not parameters:
        raise Exception("No initial parameters passed")
    
    for p in parameters: p.requires_grad = True 
    
    losses = [] 
    
    for epoch in tqdm(range(epochs)):
        
        lr = 0.1 if epoch < 100_000 else 0.01
        
        ix = torch.randint(0, X.shape[0], (bs, ))
        batch_x, batch_y = X[ix], Y[ix]
        
        logits = compute_logits_v2(parameters, batch_x)
        
        loss = F.cross_entropy(logits, batch_y)
        regularization_loss = _regularization_loss(parameters, lambdas)
        loss += regularization_loss

        for p in parameters:
            p.grad= None
            
        loss.backward()


        for index, p in enumerate(parameters):
            if p.grad is None: print(index)
            p.data += - lr * p.grad

        if enable_print and epoch % print_at_every_nth_epoch == 0: print(epoch, loss.item())
            
        losses.append(loss.item())
        
    if enable_print:  print(epoch, loss.item())   
    return losses

params8 = initilialize_parameters_v6(3, 10, 200)

len(params8)

7

losses = train_v2(params8, 200_000, Xtr, Ytr)

  0%|                                                                                                                                                                 | 104/200000 [00:00<06:19, 526.54it/s]  5%|████████                                                                                                                                                       | 10108/200000 [00:19<05:51, 539.73it/s] 10%|███████████████▉                                                                                                                                               | 20082/200000 [00:37<05:26, 550.87it/s] 15%|███████████████████████▊                                                                                                                                       | 29997/200000 [00:58<05:47, 489.55it/s] 20%|███████████████████████████████▊                                                                                                                               | 40049/200000 [01:26<09:19, 285.73it/s] 25%|███████████████████████████████████████▊                                                                                                                       | 50024/200000 [02:08<16:14, 153.85it/s] 30%|███████████████████████████████████████████████▊                                                                                                               | 60073/200000 [02:38<04:36, 505.30it/s] 35%|███████████████████████████████████████████████████████▋                                                                                                       | 70022/200000 [03:17<16:32, 130.95it/s] 40%|███████████████████████████████████████████████████████████████▋                                                                                               | 80090/200000 [03:41<04:08, 483.44it/s] 45%|███████████████████████████████████████████████████████████████████████▌                                                                                       | 90063/200000 [04:00<03:17, 557.71it/s] 50%|███████████████████████████████████████████████████████████████████████████████                                                                               | 100101/200000 [04:20<03:10, 523.81it/s] 55%|██████████████████████████████████████████████████████████████████████████████████████▉                                                                       | 110071/200000 [04:39<03:39, 410.30it/s] 60%|██████████████████████████████████████████████████████████████████████████████████████████████▊                                                               | 120058/200000 [05:16<02:55, 454.36it/s] 65%|██████████████████████████████████████████████████████████████████████████████████████████████████████▋                                                       | 130062/200000 [05:37<02:17, 506.81it/s] 70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                                               | 140096/200000 [05:56<01:53, 527.01it/s] 75%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌                                       | 150095/200000 [06:15<01:35, 525.17it/s] 80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                               | 160090/200000 [06:35<01:19, 502.85it/s] 85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                       | 170102/200000 [06:54<00:59, 501.19it/s] 90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏               | 180063/200000 [07:13<00:38, 511.77it/s] 95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏       | 190075/200000 [07:32<00:18, 540.90it/s]100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 200000/200000 [07:51<00:00, 424.08it/s]

0 3.2974765300750732
10000 2.2444629669189453
20000 2.0267117023468018
30000 2.3122177124023438
40000 1.8772399425506592
50000 1.8241453170776367
60000 2.2491812705993652
70000 2.332838535308838
80000 2.2603352069854736
90000 2.521674394607544
100000 2.1766295433044434
110000 2.0648574829101562
120000 1.9632437229156494
130000 2.6266632080078125
140000 1.9747267961502075
150000 2.2220919132232666
160000 2.2269341945648193
170000 1.8781782388687134
180000 2.018829107284546
190000 1.694084644317627
199999 1.8435885906219482

def evaluate_loss_v2(parameters, X, Y):
    logits = compute_logits_v2(parameters, X)
    return F.cross_entropy(logits, Y)

def loss_split_v2(parameters, dataset='train'):
    dataset_choices = {
        'train': (Xtr, Ytr),
        'valid': (Xdev, Ydev),
        'test': (Xte, Yte)
    }
    return evaluate_loss_v2(parameters, *dataset_choices[dataset])

loss_split_v2(params8, 'train'), loss_split_v2(params8, 'valid')

(tensor(2.0683, grad_fn=<NllLossBackward0>),
 tensor(2.1130, grad_fn=<NllLossBackward0>))

Consider the Training set mean and std deviation

def compute_batchnorm_mean_std(parameters):
    C, W1, b1, *rest = parameters
    emb = C[Xtr]
    embcat = emb.view(emb.shape[0], -1)
    hpreact = embcat @ W1 + b1
    # measure the mean/std over the training set
    bnmean = hpreact.mean(0, keepdim = True)
    bnstd = hpreact.std(0, keepdim = True)
    return bnmean, bnstd

train_bnmean, train_bnstd = compute_batchnorm_mean_std(params8)

def compute_logits_v3(parameters, X, bnmean=None, bnstd=None):
    C, W1, b1, W2, b2, bngain, bnbias = parameters
    emb = C[X]
    embcat = emb.view(-1, W1.shape[0]) 
    h_pre_act = embcat @ W1 + b1

    if  bnmean is None  and bnstd is None:
        bnmean = h_pre_act.mean(0, keepdim = True)
        bnstd = h_pre_act.std(0, keepdim = True)
        
    h_pre_act_norm = (h_pre_act - bnmean) / bnstd
    h_pre_act_scale_shift = bngain * h_pre_act_norm + bnbias
    h = torch.tanh(h_pre_act_scale_shift)
    logits = h @ W2 + b2
    return logits

def evaluate_loss_v3(parameters, X, Y, bnmean, bnstd):
    logits = compute_logits_v3(parameters, X, bnmean, bnstd)
    return F.cross_entropy(logits, Y)

def loss_split_v3(parameters, bnmean, bnstd, dataset='train'):
    dataset_choices = {
        'train': (Xtr, Ytr),
        'valid': (Xdev, Ydev),
        'test': (Xte, Yte)
    }
    return evaluate_loss_v3(parameters, *dataset_choices[dataset], bnmean, bnstd)

loss_split_v3(params8, train_bnmean, train_bnstd, 'train'), loss_split_v3(params8, train_bnmean, train_bnstd, 'valid')

(tensor(2.0683, grad_fn=<NllLossBackward0>),
 tensor(2.1131, grad_fn=<NllLossBackward0>))

Compute running mean and std

def initilialize_parameters_v7(block_size, embedding_size, hidden_neuron):
    C = torch.randn((27, embedding_size), generator=g)
    W1 = torch.randn((block_size * embedding_size, hidden_neuron), generator=g) * ((5/3) / ((embedding_size * block_size) ** 0.5))
    b1 = torch.randn(hidden_neuron, generator=g) * 0.01
    W2 = torch.randn((hidden_neuron, 27), generator=g) * 0.01
    b2 = torch.randn(27, generator=g) * 0
    
    bngain = torch.ones((1, hidden_neuron)) # for scale in batch normalization
    bnbias = torch.zeros((1, hidden_neuron)) # for shift in batch normalization
    
    bnmean_running = torch.zeros((1, hidden_neuron))
    bnstd_running = torch.ones((1, hidden_neuron))
    
    return [C, W1, b1, W2, b2, bngain, bnbias, bnmean_running, bnstd_running]

def compute_logits_v4(parameters, X, step='training'):
    C, W1, b1, W2, b2, bngain, bnbias, bnmean_running, bnstd_running = parameters
    emb = C[X]
    embcat = emb.view(-1, W1.shape[0]) 
    h_pre_act = embcat @ W1 + b1

    if step == 'training':
        bnmeani = h_pre_act.mean(0, keepdim = True)
        bnstdi = h_pre_act.std(0, keepdim = True)

        with torch.no_grad():
            bnmean_running.data = 0.999 * bnmean_running.data + 0.001 * bnmeani
            bnstd_running.data = 0.999 * bnstd_running.data + 0.001 * bnstdi
    else:
        bnmeani = bnmean_running
        bnstdi = bnstd_running
        
    h_pre_act_norm = (h_pre_act - bnmeani) / bnstdi
    h_pre_act_scale_shift = bngain * h_pre_act_norm + bnbias
    h = torch.tanh(h_pre_act_scale_shift)
    logits = h @ W2 + b2
    return logits

def train_v3(parameters,
          epochs,
          X, 
          Y, 
          bs=32, 
          lambdas = [0, 0, 0],
          enable_print=True,
          print_at_every_nth_epoch=10000
         ):
    
    if not parameters:
        raise Exception("No initial parameters passed")
    
    for p in parameters: p.requires_grad = True 
    
    losses = [] 
    
    for epoch in tqdm(range(epochs)):
        
        lr = 0.1 if epoch < 100_000 else 0.01
        
        ix = torch.randint(0, X.shape[0], (bs, ))
        batch_x, batch_y = X[ix], Y[ix]
        
        logits = compute_logits_v4(parameters, batch_x)
        
        loss = F.cross_entropy(logits, batch_y)
        regularization_loss = _regularization_loss(parameters, lambdas)
        loss += regularization_loss

        for p in parameters:
            p.grad= None
            
        loss.backward()


        for index, p in enumerate(parameters):
            if p.grad is not None: p.data += - lr * p.grad

        if enable_print and epoch % print_at_every_nth_epoch == 0: print(epoch, loss.item())
            
        losses.append(loss.item())
        
    if enable_print:  print(epoch, loss.item())   
    return losses

params9 = initilialize_parameters_v7(3, 10, 200)

losses = train_v3(params9, 200_000, Xtr, Ytr)

  0%|                                                                                                                                                                  | 53/200000 [00:00<11:28, 290.39it/s]  5%|████████                                                                                                                                                       | 10064/200000 [00:21<06:26, 491.17it/s] 10%|███████████████▉                                                                                                                                               | 20069/200000 [00:44<06:25, 466.38it/s] 15%|███████████████████████▉                                                                                                                                       | 30094/200000 [01:05<05:47, 489.06it/s] 20%|███████████████████████████████▊                                                                                                                               | 40057/200000 [01:25<05:32, 481.69it/s] 25%|███████████████████████████████████████▊                                                                                                                       | 50058/200000 [01:47<05:00, 499.70it/s] 30%|███████████████████████████████████████████████▊                                                                                                               | 60073/200000 [02:08<04:49, 483.97it/s] 35%|███████████████████████████████████████████████████████▋                                                                                                       | 70031/200000 [02:36<09:18, 232.65it/s] 40%|███████████████████████████████████████████████████████████████▋                                                                                               | 80046/200000 [03:29<06:10, 323.66it/s] 45%|████████████████████████████████████████████████████████████████████████                                                                                        | 90023/200000 [04:09<22:28, 81.54it/s] 50%|███████████████████████████████████████████████████████████████████████████████                                                                               | 100065/200000 [04:35<03:46, 440.83it/s] 55%|██████████████████████████████████████████████████████████████████████████████████████▉                                                                       | 110070/200000 [05:05<03:09, 474.93it/s] 60%|██████████████████████████████████████████████████████████████████████████████████████████████▊                                                               | 120084/200000 [05:26<02:52, 462.69it/s] 65%|██████████████████████████████████████████████████████████████████████████████████████████████████████▋                                                       | 130038/200000 [05:56<03:10, 367.74it/s] 70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                                               | 140079/200000 [06:35<02:15, 443.66it/s] 75%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌                                       | 150058/200000 [06:58<02:12, 375.75it/s] 80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍                               | 160053/200000 [07:30<01:22, 482.75it/s] 85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎                       | 170064/200000 [08:07<01:10, 422.13it/s] 90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏               | 180042/200000 [08:39<00:47, 422.86it/s] 95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏       | 190066/200000 [09:03<00:22, 440.71it/s]100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 200000/200000 [09:44<00:00, 341.89it/s]

0 3.2910704612731934
10000 2.2731170654296875
20000 2.676584482192993
30000 2.425685405731201
40000 2.1894543170928955
50000 2.406543731689453
60000 2.19313383102417
70000 1.9194616079330444
80000 2.9036688804626465
90000 2.281238079071045
100000 1.890221357345581
110000 2.034389019012451
120000 1.7974919080734253
130000 2.2577686309814453
140000 2.1341137886047363
150000 2.03934907913208
160000 2.2662088871002197
170000 2.285844564437866
180000 2.451364755630493
190000 2.512420654296875
199999 2.0207467079162598

train_bmean, train_bstd = compute_batchnorm_mean_std(params9)

train_bmean.shape

torch.Size([1, 200])

train_bstd.shape

torch.Size([1, 200])

params9[-2]

tensor([[ 0.0375, -0.6331, -0.3791, -0.9008,  0.2962,  1.4619, -0.2891,  0.1883,
          0.3329,  0.2727, -0.9458, -0.6716, -0.5048, -0.6620,  0.2342,  1.1776,
          0.5657,  1.9836, -0.2188, -0.1207, -1.8573,  0.3398,  0.3636,  2.3903,
          0.4538,  0.0833, -1.0701, -0.7340, -0.3513,  1.9030, -0.7348, -0.4769,
         -2.3932, -0.3250,  0.3072,  0.4761,  1.0564, -0.9924, -0.5760,  1.1480,
         -1.0848,  1.0707,  1.4146, -1.5361, -1.7056, -1.0768,  0.5271, -0.1483,
         -0.3467, -1.4341,  0.3082, -0.1178,  1.0577, -1.3717,  0.2063, -0.7474,
         -0.5008,  0.7797, -0.4381, -0.5850, -0.6317,  0.9563, -1.2107,  0.2256,
         -0.3417, -0.0634, -1.0470, -0.7367,  0.4666, -0.9433,  0.0427,  0.6610,
         -0.0472, -0.6191, -0.2211, -0.3358, -0.1517, -0.5254,  1.0690, -1.2109,
         -0.2712, -1.7430, -1.3447,  0.6727,  0.9114, -0.9647, -0.1962,  0.2689,
         -0.5687,  0.5511, -0.1002,  0.4604, -0.3753, -0.3717, -0.8587, -0.2480,
         -0.8048,  0.5067,  0.9874, -0.9155,  1.0679,  0.8766, -0.3299, -0.4363,
          0.4756, -0.2838, -1.1314,  0.8018,  0.0026, -0.1068, -0.7755, -0.3257,
          1.3104,  0.4733,  0.2502,  0.9611,  1.2929, -0.7287, -0.7842, -1.1771,
          0.6131, -0.4987, -0.2233, -0.0505,  0.2554, -1.3391,  0.4501, -0.6442,
         -0.2634, -0.3602,  2.0635,  0.6144, -0.2697,  1.7540, -2.0597,  0.7119,
         -0.7171, -0.0732,  0.8917,  0.1726,  0.6225, -0.5065,  1.7100, -0.0922,
          0.1529,  1.6846,  0.3420, -0.4169, -0.2356, -0.4468, -0.8213,  0.2331,
         -2.2176, -0.0141,  0.2564,  0.1819,  0.0972,  0.4663,  0.5573,  0.5170,
         -2.4660,  0.6317, -0.0866, -1.3206, -0.3167, -1.1647, -1.4368,  0.0419,
         -0.6170, -0.8835,  0.8117, -0.8902, -1.6758,  1.4599,  0.6674, -0.5737,
         -0.3982, -0.8486,  0.7648, -0.6740, -0.8773,  0.1644,  0.3821, -1.0831,
          1.0532,  0.7580, -0.5744, -0.6737, -0.6705,  0.5464,  0.3474,  0.5626,
         -0.8972, -0.6644, -0.4031, -1.2800,  1.5996, -0.8948, -1.6051, -0.8797]],
       requires_grad=True)

train_bmean

tensor([[ 0.0336, -0.6265, -0.3734, -0.9142,  0.3122,  1.4727, -0.2720,  0.2043,
          0.3280,  0.2649, -0.9420, -0.6603, -0.5234, -0.6541,  0.2307,  1.1702,
          0.5762,  1.9697, -0.2134, -0.1228, -1.8548,  0.3674,  0.3822,  2.3695,
          0.4678,  0.0884, -1.0760, -0.7574, -0.3623,  1.9024, -0.7362, -0.4469,
         -2.3866, -0.3177,  0.2965,  0.4548,  1.0385, -0.9807, -0.5685,  1.1614,
         -1.0926,  1.0664,  1.4133, -1.5146, -1.6854, -1.0843,  0.5003, -0.1437,
         -0.3558, -1.4272,  0.2930, -0.1223,  1.0598, -1.3414,  0.2255, -0.7481,
         -0.5164,  0.7950, -0.4377, -0.5765, -0.6527,  0.9657, -1.1949,  0.2556,
         -0.3367, -0.0697, -1.0539, -0.7473,  0.4742, -0.9174,  0.0496,  0.6626,
         -0.0252, -0.6193, -0.2340, -0.3298, -0.1581, -0.5270,  1.0956, -1.1991,
         -0.2696, -1.7306, -1.3725,  0.6711,  0.9122, -0.9572, -0.1943,  0.2736,
         -0.5639,  0.5646, -0.0927,  0.4803, -0.3902, -0.3292, -0.8637, -0.2507,
         -0.8104,  0.5088,  0.9935, -0.9224,  1.0957,  0.8640, -0.3443, -0.4084,
          0.4823, -0.2982, -1.1175,  0.8094,  0.0229, -0.1139, -0.7825, -0.3265,
          1.3089,  0.4729,  0.2671,  0.9844,  1.3121, -0.7067, -0.8011, -1.1575,
          0.6211, -0.5021, -0.2209, -0.0643,  0.2590, -1.3219,  0.4299, -0.6472,
         -0.2602, -0.3664,  2.0622,  0.6203, -0.2817,  1.7380, -2.0716,  0.7414,
         -0.6948, -0.0536,  0.8889,  0.1630,  0.6067, -0.5124,  1.7246, -0.0809,
          0.1703,  1.6875,  0.3339, -0.4017, -0.2522, -0.4726, -0.8133,  0.2514,
         -2.2188, -0.0041,  0.2641,  0.1699,  0.0992,  0.4487,  0.5679,  0.5218,
         -2.4712,  0.6221, -0.0852, -1.3236, -0.3386, -1.1213, -1.4408,  0.0377,
         -0.5953, -0.8718,  0.8178, -0.9079, -1.6565,  1.4652,  0.6479, -0.5730,
         -0.4037, -0.8535,  0.7510, -0.6731, -0.8535,  0.1698,  0.3929, -1.0634,
          1.0645,  0.7542, -0.5708, -0.6714, -0.6442,  0.5538,  0.3533,  0.5629,
         -0.8813, -0.6482, -0.3858, -1.2797,  1.6030, -0.8916, -1.6031, -0.8928]],
       grad_fn=<MeanBackward1>)

params9[-1]

tensor([[2.4632, 2.3683, 2.4826, 2.0530, 2.1001, 2.5936, 2.4268, 1.8161, 2.2527,
         2.2914, 2.0653, 1.7652, 2.0370, 2.3531, 2.3336, 2.2467, 2.3725, 2.4981,
         2.1250, 1.9589, 2.4479, 2.1229, 1.9701, 2.6517, 2.4070, 2.2383, 1.5956,
         1.9934, 2.2423, 2.3018, 2.1449, 1.9444, 2.1350, 2.3635, 2.1110, 2.2966,
         1.9588, 2.2902, 2.0242, 2.2285, 2.6163, 2.5771, 1.9682, 2.4096, 2.1897,
         1.9587, 2.5828, 2.2682, 1.5224, 2.2569, 2.0790, 2.0309, 2.7052, 2.0490,
         2.6919, 2.7425, 1.6170, 2.2639, 2.2183, 2.4126, 2.5572, 2.1070, 2.3111,
         2.1343, 2.4835, 1.9523, 2.4436, 2.1352, 2.6667, 2.5792, 2.4142, 2.3900,
         1.8665, 2.1212, 2.2905, 2.1226, 1.9209, 2.4108, 2.4251, 1.9492, 2.0006,
         2.7582, 2.5923, 2.1482, 1.9433, 1.8152, 2.2074, 1.9798, 2.1282, 2.5727,
         2.2498, 2.1983, 2.3262, 2.6791, 2.0241, 2.0521, 2.2381, 2.0871, 2.0417,
         2.5972, 2.0449, 2.4388, 1.9639, 2.2393, 2.1035, 2.1849, 1.9384, 2.3872,
         2.5280, 2.6528, 2.2955, 1.9553, 2.3484, 2.3475, 2.7836, 2.1356, 2.3427,
         2.0554, 2.3580, 1.9564, 2.2688, 2.2788, 2.2936, 2.1819, 2.2038, 2.3220,
         2.2896, 1.9991, 2.0549, 2.1163, 2.6239, 1.5893, 2.8965, 2.0469, 2.2779,
         2.1321, 2.1158, 1.8507, 2.3508, 1.9726, 1.9283, 2.2762, 1.9608, 2.4423,
         2.0968, 2.0759, 2.7557, 3.1357, 2.2457, 2.5234, 2.3572, 2.6196, 2.2824,
         2.1964, 2.4175, 1.3403, 2.5489, 2.2041, 2.5038, 1.9908, 2.0546, 2.3802,
         2.4392, 2.2461, 2.1533, 2.1316, 2.4615, 1.8033, 2.3087, 1.9742, 2.3235,
         1.7176, 2.0494, 2.3848, 2.3092, 2.4218, 2.2263, 2.4015, 2.1627, 2.1673,
         2.3420, 2.0868, 2.7352, 2.4064, 2.0937, 2.4994, 1.7547, 2.3966, 2.3889,
         1.9188, 2.1525, 2.0753, 2.1131, 2.1583, 2.1470, 2.2530, 2.6288, 1.9458,
         2.1839, 2.2465]], requires_grad=True)

train_bstd

tensor([[2.4732, 2.3784, 2.5213, 2.0699, 2.1313, 2.6214, 2.4610, 1.8370, 2.2874,
         2.3359, 2.0795, 1.7793, 2.0715, 2.3730, 2.3941, 2.2722, 2.4023, 2.5138,
         2.1447, 1.9971, 2.4711, 2.1447, 1.9872, 2.6469, 2.4311, 2.2664, 1.6039,
         2.0137, 2.2677, 2.3347, 2.1688, 1.9666, 2.1642, 2.4079, 2.1322, 2.3575,
         1.9967, 2.3048, 2.0512, 2.2445, 2.6568, 2.6134, 1.9959, 2.4373, 2.2055,
         1.9620, 2.6040, 2.3006, 1.5517, 2.2881, 2.1018, 2.0604, 2.7347, 2.0694,
         2.7125, 2.7579, 1.6329, 2.3031, 2.2478, 2.4416, 2.5732, 2.1449, 2.3496,
         2.1591, 2.5255, 1.9768, 2.4779, 2.1505, 2.6936, 2.5978, 2.4561, 2.3916,
         1.8887, 2.1492, 2.3122, 2.1676, 1.9488, 2.4345, 2.4486, 1.9695, 2.0231,
         2.7833, 2.6296, 2.1697, 1.9649, 1.8332, 2.2276, 1.9933, 2.1393, 2.5949,
         2.2839, 2.2298, 2.3553, 2.7204, 2.0429, 2.0738, 2.2546, 2.1089, 2.0694,
         2.6374, 2.0650, 2.4688, 1.9873, 2.2620, 2.1333, 2.2223, 1.9737, 2.4104,
         2.5586, 2.6578, 2.3239, 1.9960, 2.3708, 2.3778, 2.8150, 2.1605, 2.3796,
         2.0766, 2.3811, 1.9827, 2.2918, 2.3128, 2.3298, 2.2081, 2.2340, 2.3566,
         2.3248, 2.0105, 2.0888, 2.1318, 2.6333, 1.6082, 2.9117, 2.0752, 2.3033,
         2.1490, 2.1393, 1.8752, 2.3683, 1.9951, 1.9514, 2.3120, 1.9701, 2.4542,
         2.1293, 2.0938, 2.7844, 3.1507, 2.2620, 2.5633, 2.3879, 2.6383, 2.3134,
         2.2227, 2.4502, 1.3551, 2.5690, 2.2434, 2.5294, 2.0216, 2.0723, 2.4025,
         2.4604, 2.2773, 2.1765, 2.1551, 2.4940, 1.8347, 2.3483, 1.9932, 2.3455,
         1.7362, 2.0621, 2.4156, 2.3354, 2.4520, 2.2545, 2.4163, 2.1852, 2.1869,
         2.3587, 2.1191, 2.7597, 2.4383, 2.1112, 2.5392, 1.7744, 2.4260, 2.4106,
         1.9521, 2.1830, 2.1063, 2.1329, 2.1864, 2.1679, 2.2876, 2.6466, 1.9717,
         2.1994, 2.2678]], grad_fn=<StdBackward0>)

above values are close

def evaluate_loss_v4(parameters, X, Y, bnmean, bnstd):
    logits = compute_logits_v4(parameters, X, 'evaluation')
    return F.cross_entropy(logits, Y)

def loss_split_v4(parameters, bnmean, bnstd, dataset='train'):
    dataset_choices = {
        'train': (Xtr, Ytr),
        'valid': (Xdev, Ydev),
        'test': (Xte, Yte)
    }
    return evaluate_loss_v4(parameters, *dataset_choices[dataset], bnmean, bnstd)

loss_split_v4(params9, params9[-2], params9[-1], 'train'), loss_split_v4(params9, train_bnmean, train_bnstd, 'valid')

(tensor(2.0704, grad_fn=<NllLossBackward0>),
 tensor(2.1112, grad_fn=<NllLossBackward0>))

Pytorchifying the code

g = torch.Generator().manual_seed(2147483647)

class Linear:
    
    def __init__(self, fan_in, fan_out, bias=True):
        self.weight = torch.randn((fan_in, fan_out), generator=g) / fan_in ** 0.5
        self.bias = torch.zeros(fan_out) if bias else None
    
    def __call__(self, x):
        self.out = x @ self.weight
        if self.bias is not None:
            self.out += self.bias
        return self.out
    
    def parameters(self):
        return [self.weight] + ([] if self.bias is None else [self.bias])

class BatchNorm1d:
    
    def __init__(self, dim, eps=1e-5, momentum=0.1):
        self.eps = eps
        self.momentum = momentum
        self.training = True
        # parameters (trained with backprop)
        self.gamma = torch.ones(dim)
        self.beta = torch.zeros(dim)
        # buffers (trained with a running `monentum update`)
        self.running_mean = torch.zeros(dim)
        self.running_var  = torch.ones(dim)
    
    def __call__(self, x):
        if self.training:
            xmean = x.mean(0, keepdim=True) # batch mean
            xvar = x.var(0, keepdim=True, unbiased=True) # batch variance
        else:
            xmean = self.running_mean
            xvar = self.running_var
        
        x_hat = (x - xmean) / torch.sqrt(xvar + self.eps)
        self.out = self.gamma * x_hat + self.beta
        
        if self.training:
            with torch.no_grad():
                self.running_mean = (1 - self.momentum) * self.running_mean  + self.momentum * xmean
                self.running_var = (1 - self.momentum) * self.running_mean + self.momentum * xmean
        
        return self.out
    
    def parameters(self):
        return [self.gamma, self.beta]

class Tanh:
    def __call__(self, x):
        self.out = torch.tanh(x)
        return self.out
    def parameters(self):
        return []

def train(max_steps, X, Y, 
            bs = 32, 
            vocab_size = 27, # the number of characters
            n_embd = 10, # the dimensionality of the character embedding vectors
            n_hidden = 100, # the number of neurons in the hidden layer of the MLP
            block_size = 3, 
            weight_scale = 5/3,
            network_type = 'non-linear',
            learning_rate = None
         ):

    C = torch.randn((vocab_size, n_embd), generator=g)
    
    if network_type == 'linear':
        layers = [
            Linear(n_embd * block_size, n_hidden),
            Linear(n_hidden, n_hidden),
            Linear(n_hidden, n_hidden), 
            Linear(n_hidden, n_hidden), 
            Linear(n_hidden, n_hidden), 
            Linear(n_hidden, vocab_size)
        ]
    elif network_type == 'non-linear':
        layers = [
            Linear(n_embd * block_size, n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), Tanh(),
            Linear(n_hidden, vocab_size)
        ]
    else:
        layers = [
            Linear(n_embd * block_size, n_hidden), BatchNorm1d(n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), BatchNorm1d(n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), BatchNorm1d(n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), BatchNorm1d(n_hidden), Tanh(),
            Linear(n_hidden, n_hidden), BatchNorm1d(n_hidden), Tanh(),
            Linear(n_hidden, vocab_size), BatchNorm1d(vocab_size)
        ]
    
    with torch.no_grad():
        # last layer: make less confident
        if network_type != 'batchnorm':
            layers[-1].weight *= 0.1
        else:
            layers[-1].gamma *= 0.1
        # all other layers: apply gain
        for layer in layers[:-1]:
            if isinstance(layer, Linear):
                layer.weight *= weight_scale
                
    
    parameters = [C] + [p for layer in layers for p in layer.parameters()]
    print('Total number of parameters are :', sum(p.nelement() for p in parameters))
    for p in parameters:
        p.requires_grad = True 
        
    lossi = []
    ud = []
    for i in range(max_steps):
        # minibatch construct
        ix = torch.randint(0, X.shape[0], (bs, ), generator = g)
        Xb, Yb = X[ix], Y[ix]
        
        # forward pass
        emb = C[Xb]
        x = emb.view(emb.shape[0], -1)
        for layer in layers:
            x = layer(x)
        loss = F.cross_entropy(x, Yb)
        
        for layer in layers:
            layer.out.retain_grad() # AFTER_DEBUG: would take out retain_graph
        
        for p in parameters:
            p.grad = None
        
        loss.backward()
        
        lr = 0.1 if i < 100_000 else 0.01 # step learning rate decay
        if learning_rate: lr = learning_rate
        
        
        for p in parameters:
            p.data += -lr * p.grad
        
        # track stats
        if i % 10_000 == 0: # print every once in a while
            print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
        lossi.append(loss.log10().item())
        
        with torch.no_grad():
            ud.append([(lr * p.grad.std() / p.data.std()).log10().item() for p in parameters])
    return layers, parameters, lossi, ud

l, p, li, ud = train(1, Xtr, Ytr, network_type = 'non-linear')

Total number of parameters are : 46497
      0/      1: 3.3099

def visualize_histograms(layers, instance_layer = Tanh, output_type='forward'):
    plot.figure(figsize=(20, 4))
    legends = []
    for i, layer in enumerate(layers[:-1]):
        if isinstance(layer, instance_layer):
            if output_type == 'forward': t = layer.out
            else: t = layer.out.grad
            print('layer %d (%10s): mean %+f, std %e' % (i, layer.__class__.__name__, t.mean(), t.std()))
            hy, hx = torch.histogram(t, density=True)
            plot.plot(hx[:-1].detach(), hy.detach())
            legends.append(f'layer {i} ({layer.__class__.__name__})')
    plot.legend(legends)
    plot.title('gradient distribution')

visualize_histograms(l)

layer 1 (      Tanh): mean -0.023409, std 7.497526e-01
layer 3 (      Tanh): mean -0.002852, std 6.864228e-01
layer 5 (      Tanh): mean +0.001338, std 6.732427e-01
layer 7 (      Tanh): mean -0.006005, std 6.569249e-01
layer 9 (      Tanh): mean -0.020739, std 6.626034e-01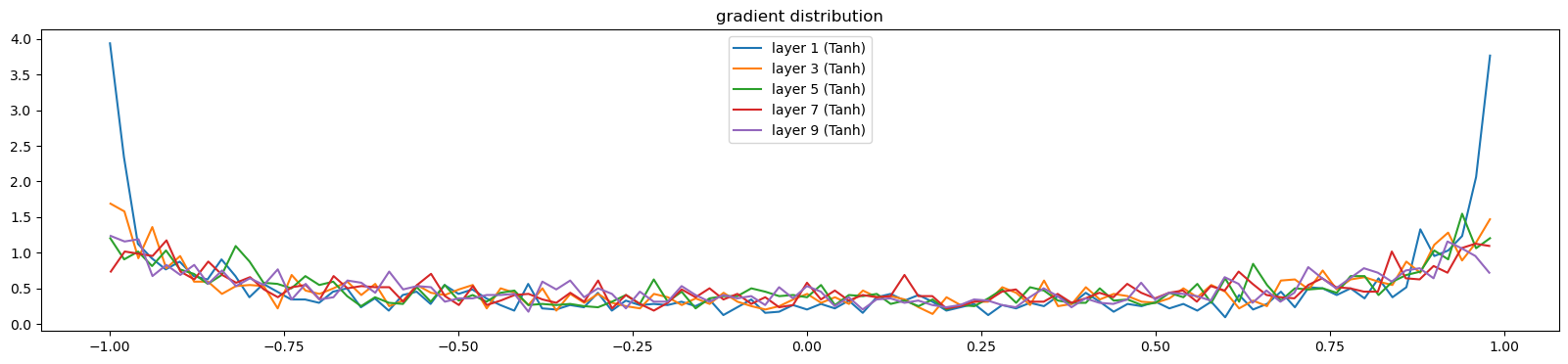

visualize_histograms(l, output_type='backward')

layer 1 (      Tanh): mean +0.000010, std 4.205588e-04
layer 3 (      Tanh): mean -0.000003, std 3.991179e-04
layer 5 (      Tanh): mean +0.000003, std 3.743020e-04
layer 7 (      Tanh): mean +0.000015, std 3.290473e-04
layer 9 (      Tanh): mean -0.000014, std 3.054035e-04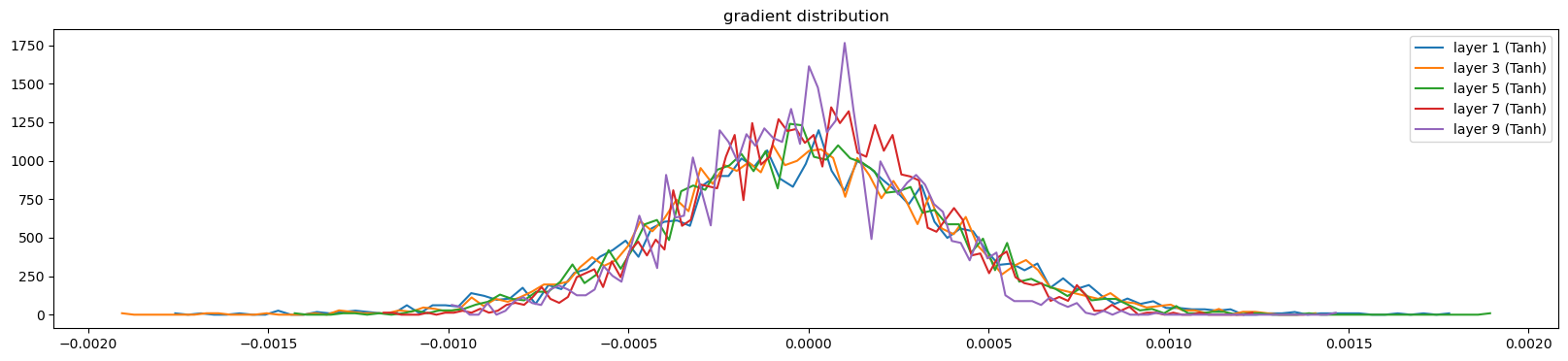

Only Non Linearities

l, p, li, ud = train(1, Xtr, Ytr, network_type='linear')

Total number of parameters are : 46497
      0/      1: 3.9508

visualize_histograms(l, instance_layer=Linear)

layer 0 (    Linear): mean -0.026808, std 1.717835e+00
layer 1 (    Linear): mean +0.066778, std 2.721437e+00
layer 2 (    Linear): mean +0.011798, std 4.644542e+00
layer 3 (    Linear): mean +0.402860, std 7.625082e+00
layer 4 (    Linear): mean +0.125483, std 1.243459e+01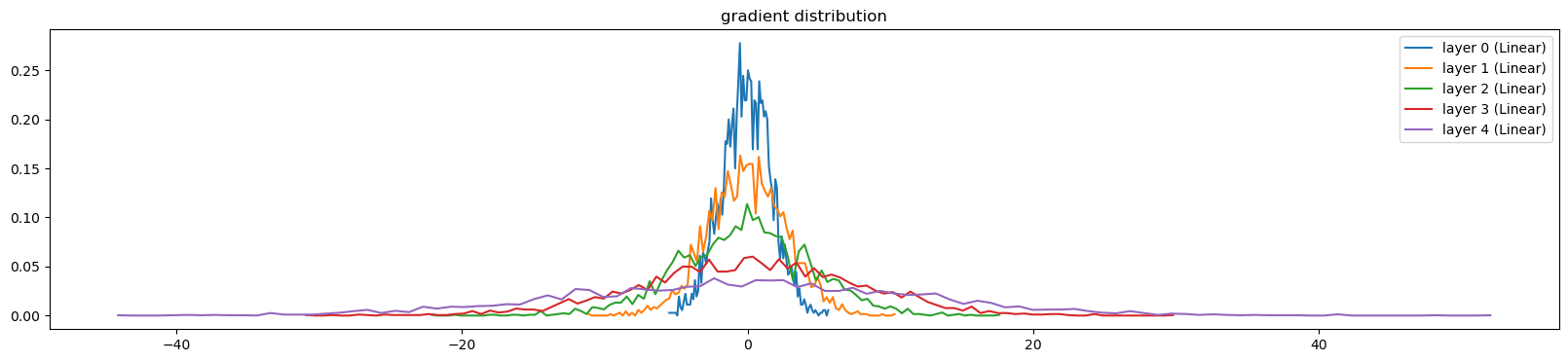

visualize_histograms(l, instance_layer=Linear, output_type='backward')

layer 0 (    Linear): mean -0.000040, std 2.520851e-03
layer 1 (    Linear): mean +0.000041, std 1.514516e-03
layer 2 (    Linear): mean +0.000030, std 9.373975e-04
layer 3 (    Linear): mean +0.000000, std 5.414668e-04
layer 4 (    Linear): mean +0.000006, std 3.237360e-04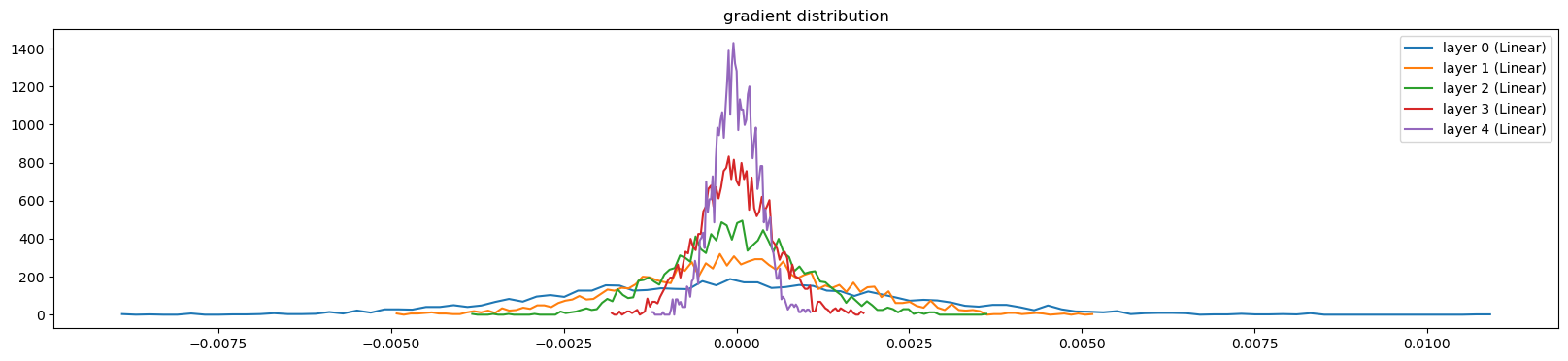

l, p, li, ud = train(1, Xtr, Ytr, weight_scale = 0.5, network_type='linear')

Total number of parameters are : 46497
      0/      1: 3.2955

visualize_histograms(l, instance_layer=Linear)

layer 0 (    Linear): mean +0.005062, std 5.380081e-01
layer 1 (    Linear): mean +0.003729, std 2.749813e-01
layer 2 (    Linear): mean +0.004225, std 1.427801e-01
layer 3 (    Linear): mean +0.000118, std 7.137968e-02
layer 4 (    Linear): mean -0.000081, std 3.339273e-02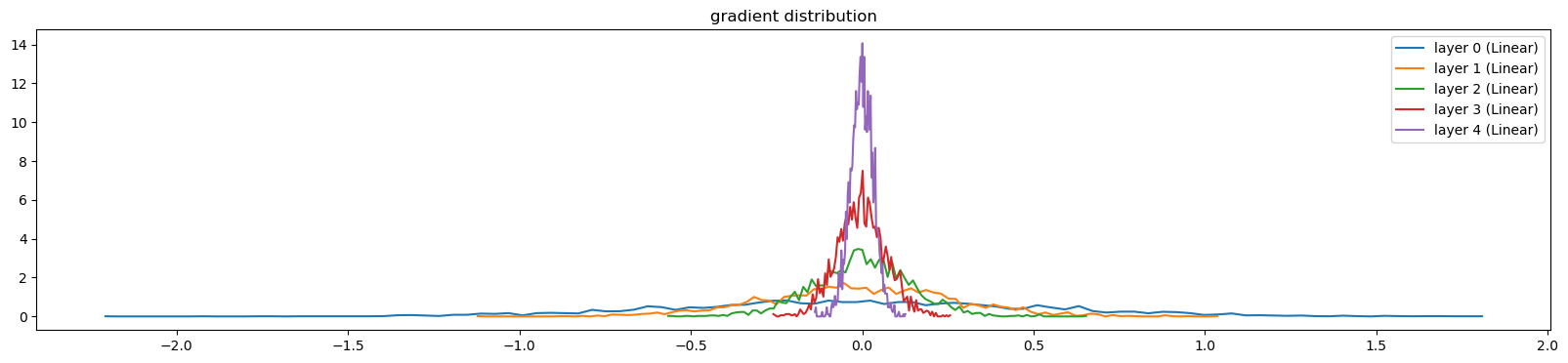

visualize_histograms(l, instance_layer=Linear, output_type='backward')

layer 0 (    Linear): mean -0.000001, std 2.208486e-05
layer 1 (    Linear): mean +0.000000, std 4.229027e-05
layer 2 (    Linear): mean +0.000002, std 8.004090e-05
layer 3 (    Linear): mean +0.000003, std 1.509417e-04
layer 4 (    Linear): mean +0.000007, std 3.050811e-04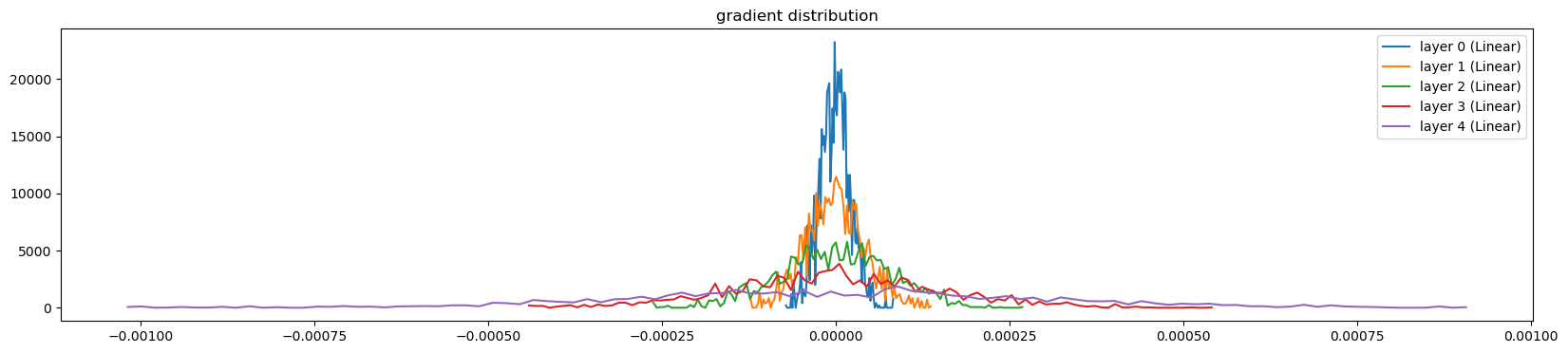

l, p, li, ud = train(1, Xtr, Ytr, weight_scale = 1, network_type='linear')

Total number of parameters are : 46497
      0/      1: 3.2962

visualize_histograms(l, instance_layer=Linear)

layer 0 (    Linear): mean -0.033228, std 1.018080e+00
layer 1 (    Linear): mean +0.032009, std 9.739050e-01
layer 2 (    Linear): mean -0.021459, std 9.661991e-01
layer 3 (    Linear): mean -0.006396, std 9.748541e-01
layer 4 (    Linear): mean +0.008816, std 1.019902e+00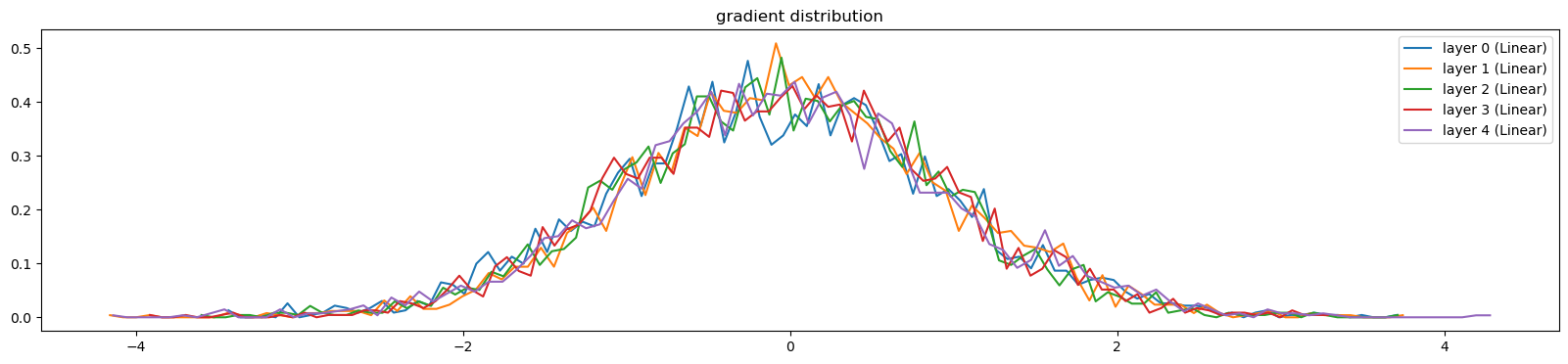

visualize_histograms(l, instance_layer=Linear, output_type='backward')

layer 0 (    Linear): mean +0.000011, std 3.135176e-04
layer 1 (    Linear): mean +0.000007, std 3.096962e-04
layer 2 (    Linear): mean -0.000003, std 3.211265e-04
layer 3 (    Linear): mean -0.000011, std 3.192310e-04
layer 4 (    Linear): mean -0.000010, std 3.158194e-04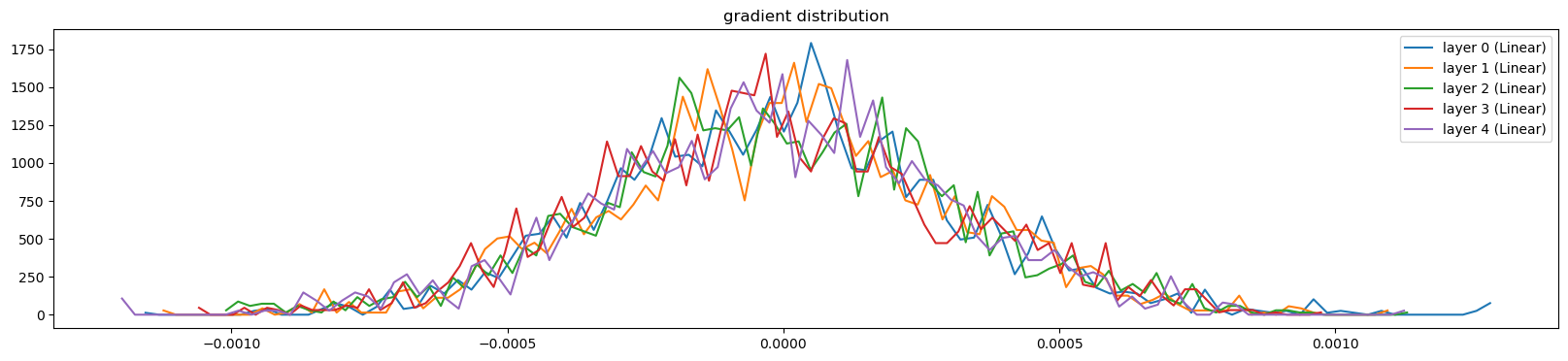

grad: data ratio

l, p, li, ud = train(1, Xtr, Ytr, weight_scale=1, network_type='linear')

Total number of parameters are : 46497
      0/      1: 3.2988

def visualize_gain_data_ratio(parameters):
    plot.figure(figsize=(20, 4))
    legends = []
    for i, p in enumerate(parameters):
        t = p.grad
        if p.ndim==2: # excluding bias, gamma, beta
            print('weight %10s | mean %+f | std %e | grad:data ratio %e' %(tuple(p.shape), t.mean(), t.std(), t.std()/p.std()))
            hy, hx = torch.histogram(t, density = True)
            plot.plot(hx[:-1].detach(), hy.detach())
            legends.append(f'{i}{tuple(p.shape)}')
    plot.legend(legends)
    plot.title('Weights gradient distribution')

visualize_gain_data_ratio(p)

weight   (27, 10) | mean -0.000028 | std 9.268780e-04 | grad:data ratio 8.800050e-04
weight  (30, 100) | mean -0.000030 | std 1.736440e-03 | grad:data ratio 9.734222e-03
weight (100, 100) | mean -0.000002 | std 1.681667e-03 | grad:data ratio 1.686680e-02
weight (100, 100) | mean +0.000011 | std 1.695616e-03 | grad:data ratio 1.695003e-02
weight (100, 100) | mean -0.000042 | std 1.680904e-03 | grad:data ratio 1.670431e-02
weight (100, 100) | mean -0.000029 | std 1.830903e-03 | grad:data ratio 1.843546e-02
weight  (100, 27) | mean -0.000000 | std 3.505145e-02 | grad:data ratio 3.360777e+00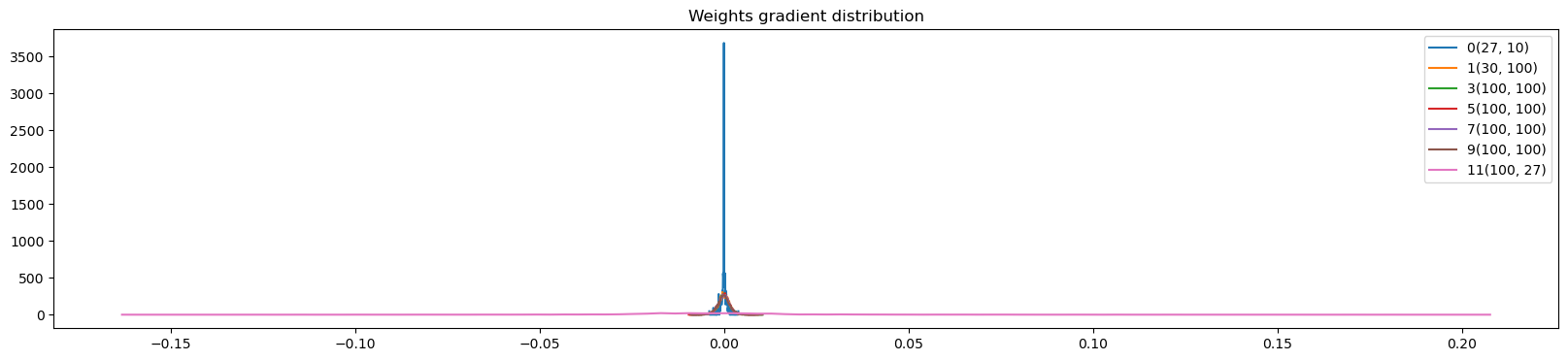

l, p, li, ud = train(1000, Xtr, Ytr, weight_scale=1, network_type='linear')

Total number of parameters are : 46497
      0/   1000: 3.2966

visualize_gain_data_ratio(p)

weight   (27, 10) | mean +0.001294 | std 1.157769e-02 | grad:data ratio 1.172457e-02
weight  (30, 100) | mean -0.000177 | std 1.309982e-02 | grad:data ratio 7.482659e-02
weight (100, 100) | mean +0.000006 | std 8.080219e-03 | grad:data ratio 8.206636e-02
weight (100, 100) | mean -0.000033 | std 6.700047e-03 | grad:data ratio 7.002961e-02
weight (100, 100) | mean +0.000095 | std 6.837256e-03 | grad:data ratio 7.082513e-02
weight (100, 100) | mean -0.000055 | std 6.807048e-03 | grad:data ratio 7.096651e-02
weight  (100, 27) | mean +0.000000 | std 2.501121e-02 | grad:data ratio 4.598068e-01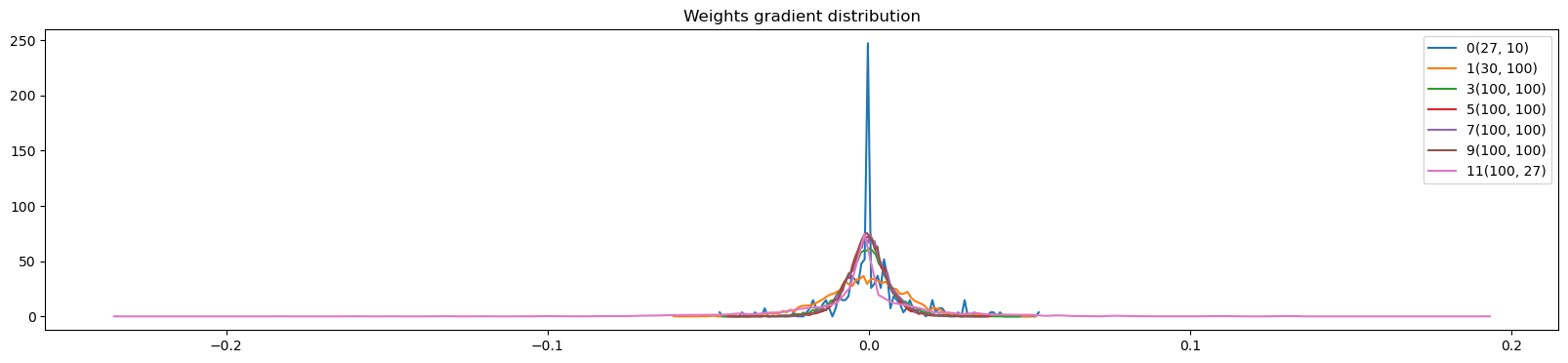

data ratio over time

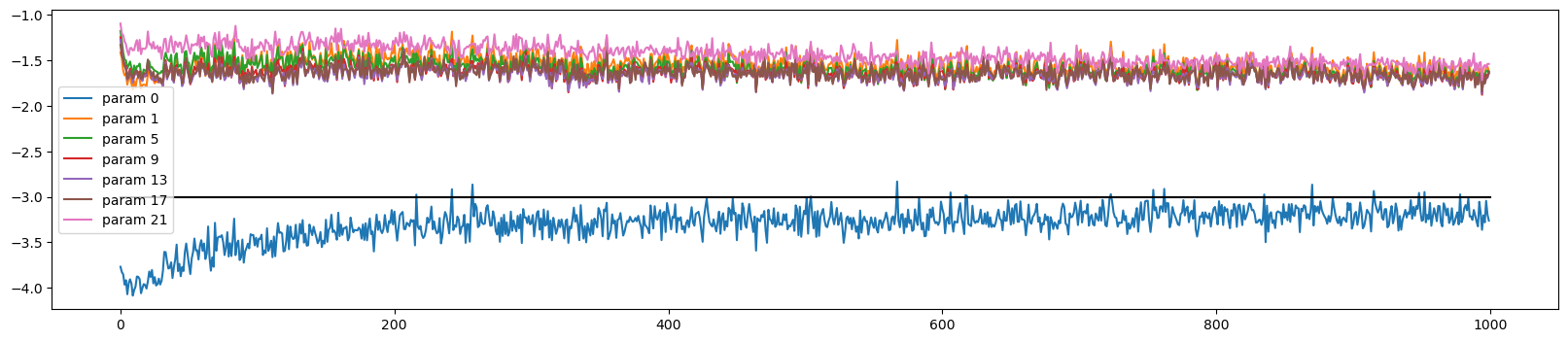
def visualize_data_ratio_over_time(parameters, ud):
    plot.figure(figsize=(20, 4))
    legends = []
    for i, p in enumerate(parameters):
        if p.ndim == 2:
            plot.plot([ud[j][i] for j in range(len(ud))])
            legends.append('param %d' % i)
    plot.plot([0, len(ud)], [-3, -3], 'k') # these ratios should be ~ 1e-3, indicate on plot
    plot.legend(legends);

visualize_data_ratio_over_time(p, ud)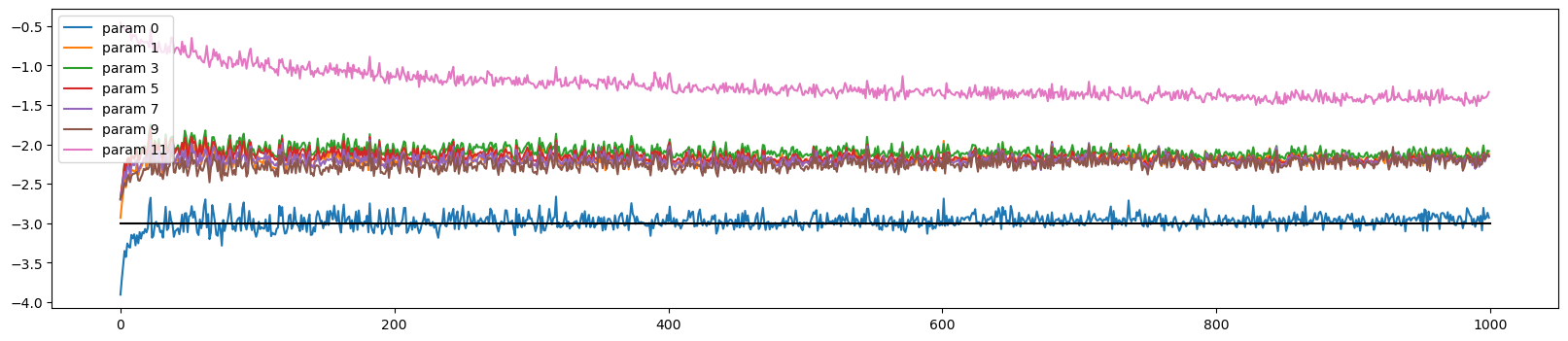

l, p, li, ud = train(1000, Xtr, Ytr, weight_scale=1, network_type='linear', learning_rate=0.001)

Total number of parameters are : 46497
      0/   1000: 3.3380

visualize_data_ratio_over_time(p, ud)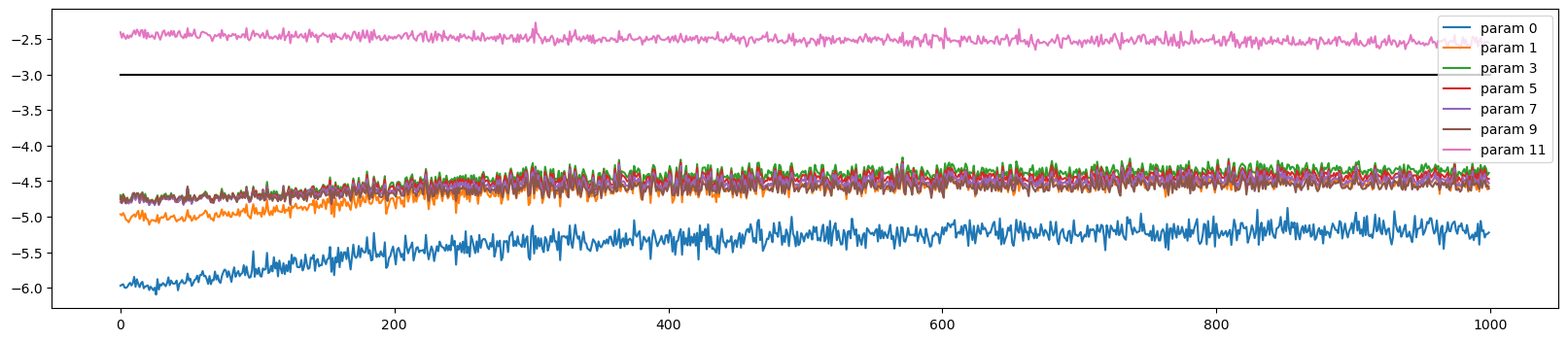

class Linear:
    
    def __init__(self, fan_in, fan_out, bias=True):
        self.weight = torch.randn((fan_in, fan_out), generator=g) #/ fan_in ** 0.5
        self.bias = torch.zeros(fan_out) if bias else None
    
    def __call__(self, x):
        self.out = x @ self.weight
        if self.bias is not None:
            self.out += self.bias
        return self.out
    
    def parameters(self):
        return [self.weight] + ([] if self.bias is None else [self.bias])

l, p, li, ud = train(1000, Xtr, Ytr)

Total number of parameters are : 46497
      0/   1000: 3.7327

visualize_data_ratio_over_time(p, ud)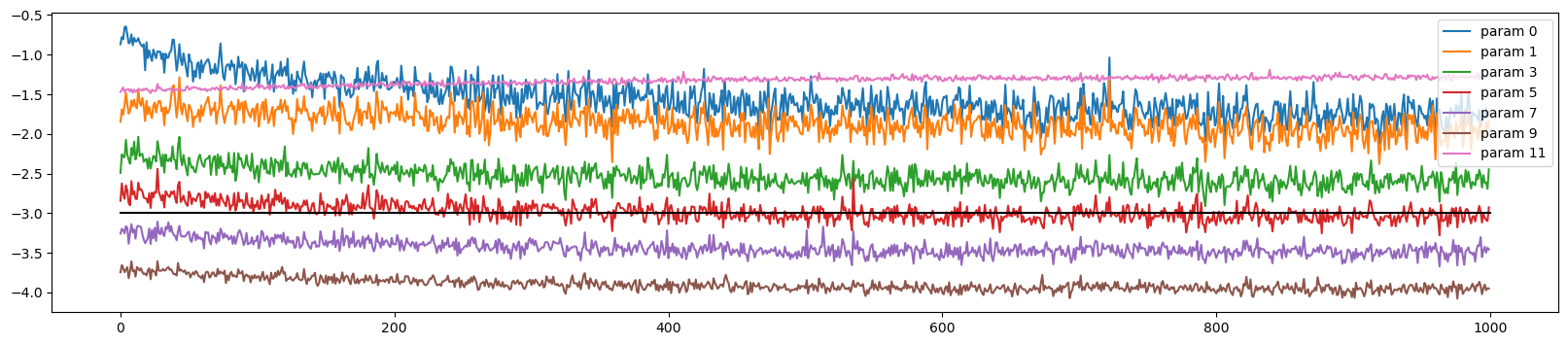

class Linear:
    
    def __init__(self, fan_in, fan_out, bias=True):
        self.weight = torch.randn((fan_in, fan_out), generator=g) / fan_in ** 0.5
        self.bias = torch.zeros(fan_out) if bias else None
    
    def __call__(self, x):
        self.out = x @ self.weight
        if self.bias is not None:
            self.out += self.bias
        return self.out
    
    def parameters(self):
        return [self.weight] + ([] if self.bias is None else [self.bias])

l, p, li, ud = train(1000, Xtr, Ytr, network_type = 'batchnorm')

Total number of parameters are : 47551
      0/   1000: 3.3050

visualize_histograms(l)

layer 2 (      Tanh): mean -0.002824, std 6.360319e-01
layer 5 (      Tanh): mean -0.003577, std 6.418643e-01
layer 8 (      Tanh): mean -0.000634, std 6.393718e-01
layer 11 (      Tanh): mean +0.004614, std 6.429055e-01
layer 14 (      Tanh): mean -0.005592, std 6.441681e-01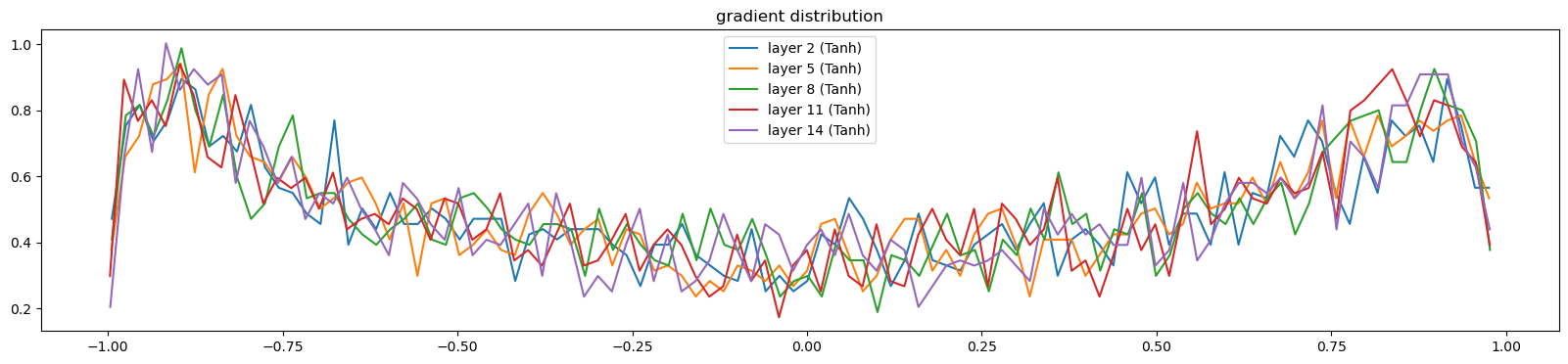

visualize_histograms(l, output_type='backward')

layer 2 (      Tanh): mean +0.000000, std 3.329200e-03
layer 5 (      Tanh): mean +0.000000, std 3.038263e-03
layer 8 (      Tanh): mean -0.000000, std 2.737059e-03
layer 11 (      Tanh): mean +0.000000, std 2.601666e-03
layer 14 (      Tanh): mean -0.000000, std 2.437597e-03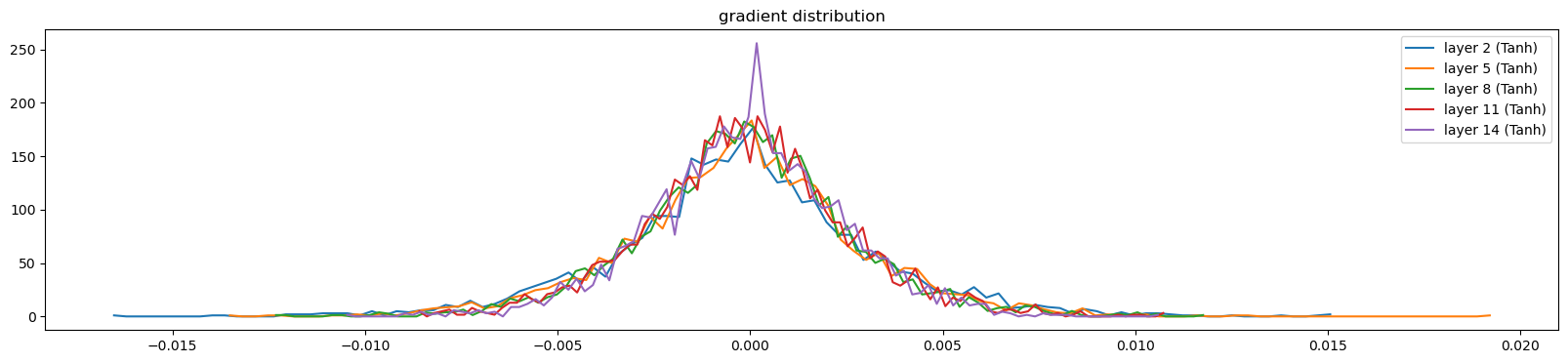

visualize_data_ratio_over_time(p, ud)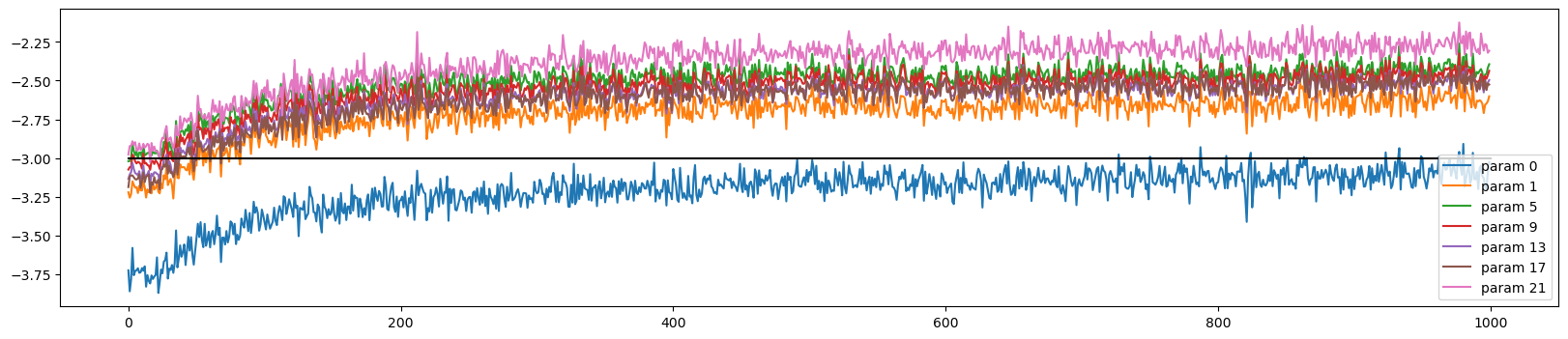

l, p, li, ud = train(1000, Xtr, Ytr, weight_scale=0.2, network_type = 'batchnorm')

Total number of parameters are : 47551
      0/   1000: 3.2990

visualize_histograms(l)

layer 2 (      Tanh): mean -0.001280, std 6.382423e-01
layer 5 (      Tanh): mean +0.004930, std 6.569912e-01
layer 8 (      Tanh): mean -0.003945, std 6.697033e-01
layer 11 (      Tanh): mean -0.000414, std 6.793090e-01
layer 14 (      Tanh): mean -0.002082, std 6.810060e-01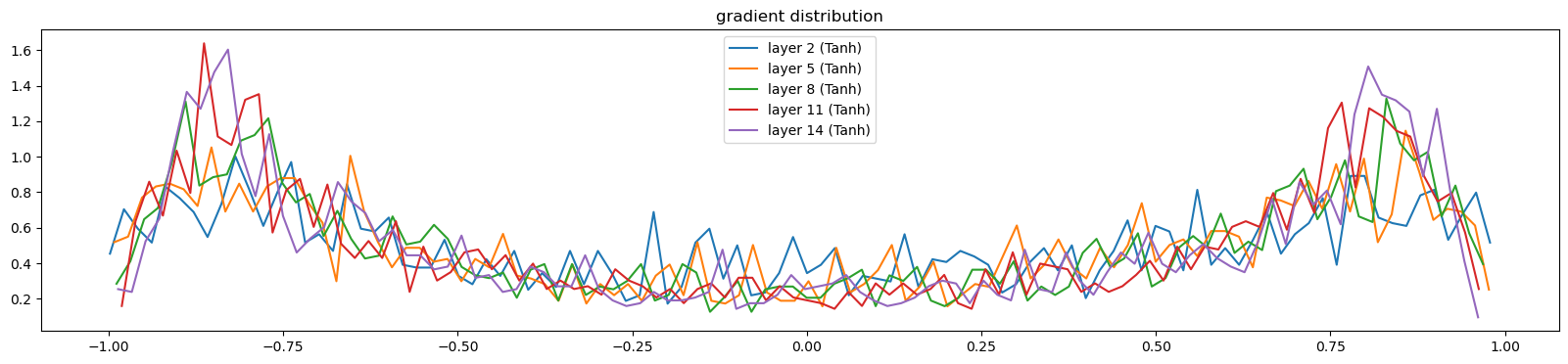

visualize_histograms(l, output_type='backward')

layer 2 (      Tanh): mean -0.000000, std 1.021346e-03
layer 5 (      Tanh): mean -0.000000, std 8.389445e-04
layer 8 (      Tanh): mean +0.000000, std 8.275748e-04
layer 11 (      Tanh): mean +0.000000, std 8.728803e-04
layer 14 (      Tanh): mean +0.000000, std 1.020851e-03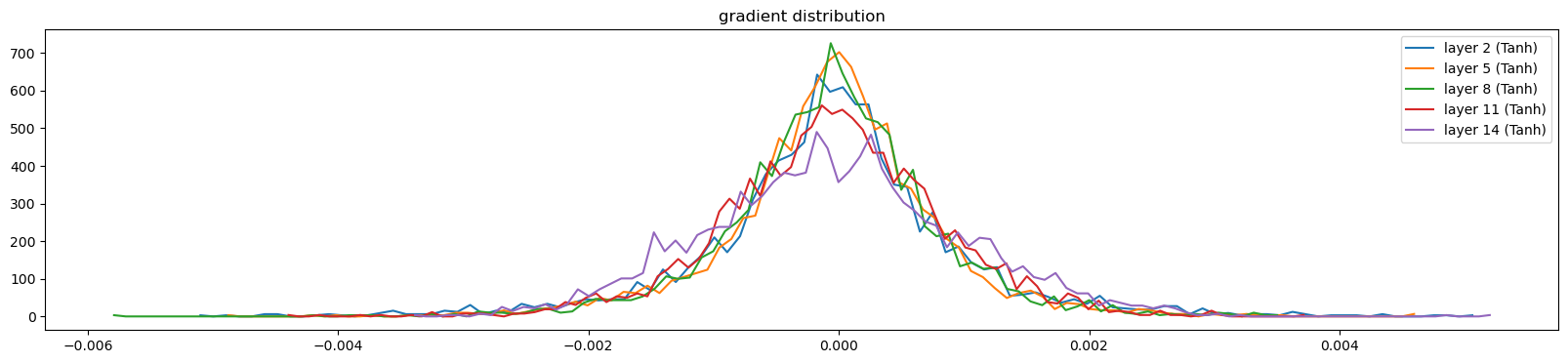

visualize_data_ratio_over_time(p, ud)