Mircrograd from scratch

import math
import numpy as np
import matplotlib.pyplot as plt
from rich import print
from rich import pretty

pretty.install()

Single Variable: x

Create a function

def f(x): return 3*x**2 - 4*x + 5

f(3.0)

20.0

xs = np.arange(-5, 5, 0.25)
xs

array([-5.  , -4.75, -4.5 , -4.25, -4.  , -3.75, -3.5 , -3.25, -3.  ,
       -2.75, -2.5 , -2.25, -2.  , -1.75, -1.5 , -1.25, -1.  , -0.75,
       -0.5 , -0.25,  0.  ,  0.25,  0.5 ,  0.75,  1.  ,  1.25,  1.5 ,
        1.75,  2.  ,  2.25,  2.5 ,  2.75,  3.  ,  3.25,  3.5 ,  3.75,
        4.  ,  4.25,  4.5 ,  4.75])

ys = f(xs)
ys

array([100.    ,  91.6875,  83.75  ,  76.1875,  69.    ,  62.1875,
        55.75  ,  49.6875,  44.    ,  38.6875,  33.75  ,  29.1875,
        25.    ,  21.1875,  17.75  ,  14.6875,  12.    ,   9.6875,
         7.75  ,   6.1875,   5.    ,   4.1875,   3.75  ,   3.6875,
         4.    ,   4.6875,   5.75  ,   7.1875,   9.    ,  11.1875,
        13.75  ,  16.6875,  20.    ,  23.6875,  27.75  ,  32.1875,
        37.    ,  42.1875,  47.75  ,  53.6875])

Plot the function

plt.plot(xs, ys)

[<matplotlib.lines.Line2D object at 0x7fb25cd152d0>]

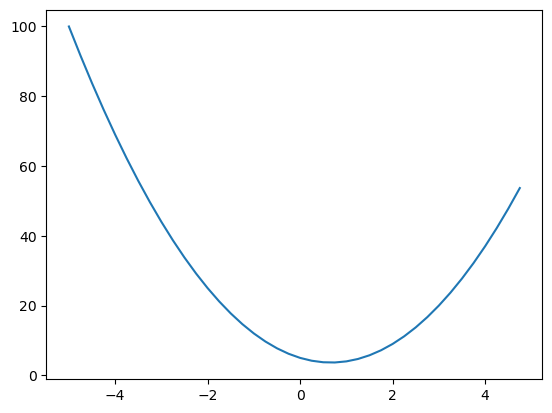
Derivative on increasing side of the curve

h = 0.0000000001
x = 3.0
(f(x + h) - f(x))/h

14.000001158365194

Derivative on the decreasing side of the curve

h = 0.0000000001
x = -3.0
(f(x + h) - f(x))/h

-21.999966293151374

Derivative on the bottom of the curve

h = 0.0000000001
x = 2/3
(f(x + h) - f(x))/h

0.0

Multivariable: a, b, c

a = 2.0
b = -3.0
c = 10.0
def d(a, b, c): return a*b + c
print(d(a, b, c))

4.0

Derivative with respect to a

h = 0.0001

a = 2.0
b = -3.0
c = 10.0

d1 = d(a, b, c)

a += h
d2 = d(a, b, c)


print('d1', d1)
print('d2', d2)
print('slope', (d2 - d1)/h)

d1 4.0

d2 3.999699999999999

slope -3.000000000010772

Derivative with respect to b

h = 0.0001

a = 2.0
b = -3.0
c = 10.0

d1 = d(a, b, c)

b += h
d2 = d(a, b, c)


print('d1', d1)
print('d2', d2)
print('slope', (d2 - d1)/h)

d1 4.0

d2 4.0002

slope 2.0000000000042206

Derivative with respect to c

h = 0.0001

a = 2.0
b = -3.0
c = 10.0

d1 = d(a, b, c)

c += h
d2 = d(a, b, c)


print('d1', d1)
print('d2', d2)
print('slope', (d2 - d1)/h)

d1 4.0

d2 4.0001

slope 0.9999999999976694

Create Value Object

(mentioned in the README of micrograd )

Define intial template of Value Class

class Value:
    def __init__(self, data):
        self.data = data

    def __repr__(self):
        return f"Value(data={self.data})"

a = Value(2.0)
b = Value(-3.0)
a, b

(Value(data=2.0), Value(data=-3.0))

Add the add function

class Value:
    def __init__(self, data):
        self.data = data

    def __repr__(self):
        return f"Value(data={self.data})"

    def __add__(self, other): # ⭠ for adding among the value objects
        return Value(self.data + other.data)

a = Value(2.0)
b = Value(-3.0)
a, b

(Value(data=2.0), Value(data=-3.0))

a + b # a.__add__(b)

Value(data=-1.0)

Add the mul function

class Value:
    def __init__(self, data):
        self.data = data

    def __repr__(self):
        return f"Value(data={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data)

    def __mul__(self, other): # ⭠ for multiplying among the value objects
        return Value(self.data * other.data)

a = Value(2.0)
b = Value(-3.0)
a, b

(Value(data=2.0), Value(data=-3.0))

a * b # a.__mul__(b)

Value(data=-6.0)

c = Value(10.0)

d = a * b + c; d

Value(data=4.0)

Add the functionality to know what values created a value with _children

class Value:
    def __init__(self, data, _children=()): # ⭠ Add _children
        self.data = data
        self._prev = set(_children) # ⭠ Add _children

    def __repr__(self):
        return f"Value(data ={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data, (self, other))

    def __mul__(self, other):
        return Value(self.data * other.data, (self, other))

a = Value(2.0)
b = Value(-3.0)
c = Value(10.0)
d = a*b + c
d

Value(data =4.0)

d._prev # childrens are -6.0 (a *b) and 10.0 (c)

{Value(data =-6.0), Value(data =10.0)}

Add the functionality to know what operations created a value with _op

class Value:
    def __init__(self, data, _children=(), _op=''): # ⭠ Add _op
        self.data = data
        self._prev = set(_children)
        self._op = _op # ⭠ Add _op

    def __repr__(self):
        return f"Value(data={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data, (self, other), '+')

    def __mul__(self, other):
        return Value(self.data * other.data, (self, other), '*')

a = Value(2.0)
b = Value(-3.0)
c = Value(10.0)
d = a*b + c
d

Value(data=4.0)

d._prev

{Value(data=10.0), Value(data=-6.0)}

d._op

'+'

Visualize the expression graph with operators and operands

from graphviz import Digraph

def trace(root):
    # build a set of all nodes and edges in a graph
    nodes, edges = set(), set()
    def build(v):
        if v not in nodes:
            nodes.add(v)
            for child in v._prev:
                edges.add((child, v))
                build(child)
    build(root)
    return nodes, edges

def draw_dot(root, label):
    dot = Digraph(format='svg', graph_attr={'rankdir': 'LR'}) # LR = left to right

    nodes, edges = trace(root)
    for n in nodes:
        uid = str(id(n))
        # for any value in the graph, create a rectangular ('record') node for it
        dot.node(name = uid, label=label(n), shape='record') # ⭠ label function getting called
        if n._op:
            # if this value is a result of some operation, create an op node for it
            dot.node(name = uid + n._op, label = n._op)
            dot.edge(uid + n._op, uid)
  
    for n1, n2 in edges:
        # connect n1 to the op node of n2
        dot.edge(str(id(n1)), str(id(n2)) + n2._op)
  
    return dot

def label(node): return "{data %.4f}" % (node.data)
draw_dot(d, label)

Add label to each node

so that we know what are the corresponding variables for each value

class Value:
    def __init__(self, data, _children=(), _op='', label=''): # ⭠ Add label
        self.data = data
        self._prev = set(_children)
        self._op = _op
        self.label = label # ⭠ Add label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data, (self, other), '+')

    def __mul__(self, other):
        return Value(self.data * other.data, (self, other), '*')

a = Value(2.0, label = 'a')
b = Value(-3.0, label='b')
c = Value(10, label = 'c')
e = a*b; e.label = 'e'
d = e + c; d.label = 'd'
f = Value(-2.0, label='f')
L = d * f; L.label = 'L'
L

Value(label=L data=-8.0)

Change the label function to render the label

def label(node): return "{%s | {data %.4f}}" % (node.label, node.data)

draw_dot(L, label)

Add grad to Value class

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data, (self, other), '+')

    def __mul__(self, other):
        return Value(self.data * other.data, (self, other), '*')

a = Value(2.0, label = 'a')
b = Value(-3.0, label='b')
c = Value(10, label = 'c')
e = a*b; e.label = 'e'
d = e + c; d.label = 'd'
f = Value(-2.0, label='f')
L = d * f; L.label = 'L'
L.grad

0.0

def label(node): return "{%s | {data %.4f} | grad %.4f}" % (node.label, node.data, node.grad)

draw_dot(L, label)

Create a function lol

Derive with respect to a

def lol():
    h = 0.0001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0 + h, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

6.000000000021544

Derive with respect to L

def lol():
    h = 0.0001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data + h

    print((L2 - L1) / h)

lol()

0.9999999999976694

L.grad = 1

draw_dot(L, label)

Derivative of L with respect to f

\[ L = f \cdot d \]

\[ \frac{\partial L}{\partial f} = \frac{\partial (f \cdot d)}{\partial f} = d = 4.0 \]

def lol():
    h = 0.001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0 + h, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

3.9999999999995595

f.grad = 4

draw_dot(L, label)

Derivative of L with respect to d

\[ \frac{\partial L}{\partial d} = \frac{\partial (f \cdot d)}{\partial d} = f = -2.0 \]

def lol():
    h = 0.001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    d.data += h
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

-2.000000000000668

d.grad = -2

draw_dot(L, label)

Derivative of L with respect to c

\[ \frac{\partial d}{\partial c} = \frac{\partial (c + e)}{\partial c} = 1.0 \]

\[ \frac{\partial L}{\partial c} = \frac{\partial L}{\partial d}\cdot\frac{\partial d}{\partial c} = f = -2.0 \]

def lol():
    h = 0.001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10 + h, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

-1.9999999999988916

c.grad = -2

draw_dot(L, label)

Derivative of L with respect to e

\[ \frac{\partial d}{\partial e} = \frac{\partial (c + e)}{\partial e} = 1.0 \]

\[ \frac{\partial L}{\partial e} = \frac{\partial L}{\partial d} \cdot \frac{\partial d}{\partial e} = f = -2.0 \]

def lol():
    h = 0.001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    e.data += h
    
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

-2.000000000000668

e.grad = -2

draw_dot(L, label)

Derivative of L with respect to a

\[ \frac{\partial e}{\partial a} = \frac{\partial ({a}\cdot{b})}{\partial a} = b \]

\[ \frac{\partial L}{\partial a} = \frac{\partial L}{\partial e} \cdot \frac{\partial e}{\partial a} = -2b = 6 \]

def lol():
    h = 0.001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0 + h, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

6.000000000000227

a.grad = 6

draw_dot(L, label)

Derivative of L with respect to b

\[ \frac{\partial e}{\partial b} = \frac{\partial ({a}\cdot{b})}{\partial b} = a \]

\[ \frac{\partial L}{\partial b} = \frac{\partial L}{\partial e} \cdot \frac{\partial e}{\partial b}= -2a = -4 \]

def lol():
    h = 0.001

    a = Value(2.0, label = 'a')
    b = Value(-3.0, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data 

    a = Value(2.0, label = 'a')
    b = Value(-3.0 + h, label='b')
    c = Value(10, label = 'c')
    e = a*b; e.label = 'e'
    
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L2 = L.data

    print((L2 - L1) / h)

lol()

-3.9999999999995595

b.grad = -4

draw_dot(L, label)

a.data += 0.01 * a.grad
b.data += 0.01 * b.grad
c.data += 0.01 * c.grad
f.data += 0.01 * f.grad

e = a * b
d = e + c
L = d * f
print(L.data)

-7.286496

Neural Network

Tanh

plt.plot(np.arange(-5, 5, 0.2), np.tanh(np.arange(-5, 5, 0.2))); plt.grid();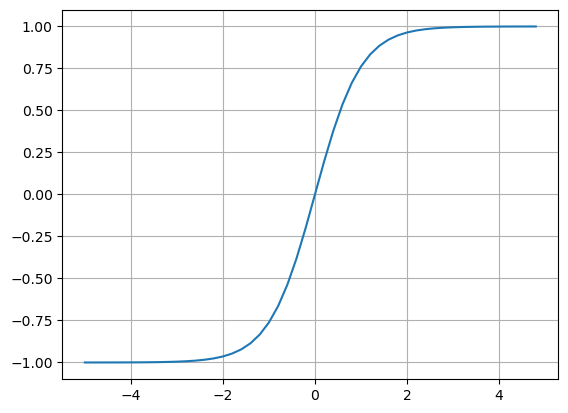

Add tanh

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        return Value(self.data + other.data, (self, other), '+')

    def __mul__(self, other):
        return Value(self.data * other.data, (self, other), '*')
    
    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        out = Value(t, (self,), 'tanh')
        return out

Inputs: x1, x2

x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

Weights: w1, w2

w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

Bias

b = Value(6.8813735870195432, label='b')

x1w1 + x2w2 + b

x1w1 = x1*w1; x1w1.label='x1*w1'
x2w2 = x2*w2; x2w2.label='x2*w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label='x1*w1 + x2*w2'
n = x1w1x2w2 + b; n.label='n'

o = n.tanh(); o.label = 'o'

draw_dot(o, label)

Computing gradient of each node manually

\[ \frac{\partial o}{\partial o} = 1 \]

o.grad = 1.0

draw_dot(o, label)

\[ o = \tanh(n) \] \[ \frac{\partial o}{\partial n} = \frac{\partial{\tanh(n)}}{\partial n} = 1 - \tanh(n)^2 = 1 - o^2 \]

1 - (o.data ** 2)

0.4999999999999999

n.grad = 0.5

draw_dot(o, label)

With pluses as we saw the gradient will be same as previous gradient

x1w1x2w2.grad = 0.5
b.grad = 0.5

draw_dot(o, label)

x1w1.grad = 0.5
x2w2.grad = 0.5

draw_dot(o, label)

x2.grad = w2.data * x2w2.grad
w2.grad = x2.data * x2w2.grad

draw_dot(o, label)

x1.grad = w1.data * x1w1.grad
w1.grad = x1.data * x1w1.grad

draw_dot(o, label)

Computing gradient of each node with _backward()

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._backward = lambda : None
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        out = Value(self.data + other.data, (self, other), '+')
        def _backward():
            self.grad = 1.0 * out.grad
            other.grad = 1.0 * out.grad
        out._backward = _backward
        return out
        
    def __mul__(self, other):
        out = Value(self.data * other.data, (self, other), '*')
        def _backward():
            self.grad = other.data * out.grad
            other.grad = self.data * out.grad
        out._backward = _backward
        return out
    
    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        out = Value(t, (self,), 'tanh')
        
        def _backward():
            self.grad = (1 - t**2) * out.grad
        out._backward = _backward
        return out

Lets take the NN code from the above

x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

b = Value(6.8813735870195432, label='b')

x1w1 = x1*w1; x1w1.label='x1*w1'
x2w2 = x2*w2; x2w2.label='x2*w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label='x1*w1 + x2*w2'
n = x1w1x2w2 + b; n.label='n'
o = n.tanh(); o.label = 'o'

draw_dot(o, label)

Backward on o

o.grad = 1.0 # setting this to 1 because Value's grad variable is 0
o._backward();  n.grad

0.4999999999999999

Backward on n

n._backward(); 
b.grad, x1w1x2w2.grad

(0.4999999999999999, 0.4999999999999999)

Backward on b

b._backward();

Backward on x1w1x2w2

x1w1x2w2._backward(); 
x1w1.grad, x2w2.grad

(0.4999999999999999, 0.4999999999999999)

Backward on x2w2

x2w2._backward()
x2.grad, w2.grad

(0.4999999999999999, 0.0)

Backward on x1w1

x1w1._backward()
x1.grad, w1.grad

(-1.4999999999999996, 0.9999999999999998)

Draw the computation graph

draw_dot(o, label)

Backward propogation with one call

x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

b = Value(6.8813735870195432, label='b')

x1w1 = x1*w1; x1w1.label='x1*w1'
x2w2 = x2*w2; x2w2.label='x2*w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label='x1*w1 + x2*w2'
n = x1w1x2w2 + b; n.label='n'
o = n.tanh(); o.label = 'o'

draw_dot(o, label)

Topological sort

topo = []
visited = set()
def build_topo(v):
    if v not in visited:
        visited.add(v)
        for child in v._prev:
            build_topo(child)
        topo.append(v)
build_topo(o)
topo

[
    Value(label=x1 data=2.0),
    Value(label=w1 data=-3.0),
    Value(label=x1*w1 data=-6.0),
    Value(label=w2 data=1.0),
    Value(label=x2 data=0.0),
    Value(label=x2*w2 data=0.0),
    Value(label=x1*w1 + x2*w2 data=-6.0),
    Value(label=b data=6.881373587019543),
    Value(label=n data=0.8813735870195432),
    Value(label=o data=0.7071067811865476)
]

Apply backward in reverse order of topological order of the computation graph

for node in reversed(topo):
    node._backward()

draw_dot(o, label)

Add backward to Value

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._backward = lambda : None
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        out = Value(self.data + other.data, (self, other), '+')
        def _backward():
            self.grad = 1.0 * out.grad
            other.grad = 1.0 * out.grad
        out._backward = _backward
        return out
        
    def __mul__(self, other):
        out = Value(self.data * other.data, (self, other), '*')
        def _backward():
            self.grad = other.data * out.grad
            other.grad = self.data * out.grad
        out._backward = _backward
        return out
    
    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        out = Value(t, (self,), 'tanh')
        
        def _backward():
            self.grad = (1 - t**2) * out.grad
        out._backward = _backward
        return out

    def backward(self):
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)
        
        self.grad = 1.0
        for node in reversed(topo):
            node._backward()

x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

b = Value(6.8813735870195432, label='b')

x1w1 = x1*w1; x1w1.label='x1*w1'
x2w2 = x2*w2; x2w2.label='x2*w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label='x1*w1 + x2*w2'
n = x1w1x2w2 + b; n.label='n'
o = n.tanh(); o.label = 'o'

o.backward()

draw_dot(o, label)

Fixing a backprop bug

a = Value(3.0, label='b')
b = a + a; b.label = 'b'
b.backward()
draw_dot(b, label)

a = Value(-2.0, label='a')
b = Value(3.0, label='b')
d = a*b; d.label = 'd'
e = a+b; e.label = 'e'
f = d*e; f.label = 'f'
f.backward()
draw_dot(f, label)

Accumulate the gradient

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._backward = lambda : None
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        out = Value(self.data + other.data, (self, other), '+')
        def _backward():
            self.grad += 1.0 * out.grad # <- Accumulate the gradient
            other.grad += 1.0 * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out
        
    def __mul__(self, other):
        out = Value(self.data * other.data, (self, other), '*')
        def _backward():
            self.grad += other.data * out.grad # <- Accumulate the gradient
            other.grad += self.data * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out
    
    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        out = Value(t, (self,), 'tanh')
        
        def _backward():
            self.grad += (1 - t**2) * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out

    def backward(self):
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)
        
        self.grad = 1.0
        for node in reversed(topo):
            node._backward()

a = Value(3.0, label='b')
b = a + a; b.label = 'b'
b.backward()
draw_dot(b, label)

a = Value(-2.0, label='a')
b = Value(3.0, label='b')
d = a*b; d.label = 'd'
e = a+b; e.label = 'e'
f = d*e; f.label = 'f'
f.backward()
draw_dot(f, label)

Add and multiply Value object with constant

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._backward = lambda : None
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other), '+')
        def _backward():
            self.grad += 1.0 * out.grad # <- Accumulate the gradient
            other.grad += 1.0 * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out
    
    def __radd__(self, other): # other + self
        return self + other
        
    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*')
        def _backward():
            self.grad += other.data * out.grad # <- Accumulate the gradient
            other.grad += self.data * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out
    
    def __rmul__(self, other): # other * self
        return self * other
    
    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        out = Value(t, (self,), 'tanh')
        
        def _backward():
            self.grad += (1 - t**2) * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out

    def backward(self):
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)
        
        self.grad = 1.0
        for node in reversed(topo):
            node._backward()

a = Value(2.0); a + 1

Value(label= data=3.0)

a = Value(2.0); a * 1

Value(label= data=2.0)

2 * a

Value(label= data=4.0)

2 + a

Value(label= data=4.0)

Implement tanh

class Value:
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # ⭠ Add grad
        self._backward = lambda : None
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        return f"Value(label={self.label} data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other), '+')
        def _backward():
            self.grad += 1.0 * out.grad # <- Accumulate the gradient
            other.grad += 1.0 * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out
    
    def __radd__(self, other): # other + self
        return self + other
        
    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*')
        def _backward():
            self.grad += other.data * out.grad # <- Accumulate the gradient
            other.grad += self.data * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out
    
    def __rmul__(self, other): # other * self
        return self * other
    
    def __pow__(self, other):
        assert isinstance(other, (int, float)), "only supporting int/float powers for now"
        out = Value(self.data ** other, (self,), f'**{other}')
        
        def _backward():
            self.grad += other * (self.data ** (other - 1)) * out.grad
        out._backward = _backward
        
        return out
        
    
    def exp(self):
        x = self.data
        out = Value(math.exp(x), (self,), 'exp')
        
        def _backward():
            self.grad += out.data * out.grad
        out._backward = _backward
        return out
    
    def __truediv__(self, other): # self / other
        return self * other**-1
    
    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)
        out = Value(t, (self,), 'tanh')
        
        def _backward():
            self.grad += (1 - t**2) * out.grad # <- Accumulate the gradient
        out._backward = _backward
        return out

    def __neg__(self): #-self
        return -self
    
    def __sub__(self, other): # self - other
        return self + (-other)
        
    def backward(self):
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)
        
        self.grad = 1.0
        for node in reversed(topo):
            node._backward()

a = Value(2.0)

a.exp()

Value(label= data=7.38905609893065)

b = Value(3.0)

a/b

Value(label= data=0.6666666666666666)

a **4

Value(label= data=16.0)

a - 1

Value(label= data=1.0)

x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

b = Value(6.8813735870195432, label='b')

x1w1 = x1*w1; x1w1.label='x1*w1'
x2w2 = x2*w2; x2w2.label='x2*w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label='x1*w1 + x2*w2'
n = x1w1x2w2 + b; n.label='n'
# -----
e = (2*n).exp()
o = (e - 1)/(e + 1)
# -----
o.label = 'o'
o.backward()
draw_dot(o, label)

x1w1 + x2w2 + b with PyTorch

import torch

x1 = torch.Tensor([2.0]).double(); x1.requires_grad = True
x2 = torch.Tensor([0.0]).double(); x2.requires_grad = True
w1 = torch.Tensor([-3.0]).double(); w1.requires_grad = True
w2 = torch.Tensor([1.0]).double(); w2.requires_grad = True
b = torch.Tensor([6.8813735870195432]); b.requires_grad = True
n = x1*w1 + x2*w2 + b
o = torch.tanh(n)

print(o.data.item())
o.backward()

print('-----')
print('x2', x2.grad.item())
print('w2', w2.grad.item())
print('x1', x1.grad.item())
print('w1', w1.grad.item())

0.7071066904050358

-----

x2 0.5000001283844369

w2 0.0

x1 -1.5000003851533106

w1 1.0000002567688737

torch.Tensor([[1, 2, 3], [4, 5, 6]])

tensor([[1., 2., 3.],
        [4., 5., 6.]])

Neural Network

import random

class Neuron:
    def __init__(self, nin):
        self.w = [Value(random.uniform(-1, 1)) for _ in range(nin)]
        self.b = Value(random.uniform(-1, 1))
    
    def __call__(self, x):
        act =  sum((wi*xi for wi, xi in zip(self.w, x)), self.b)
        return act.tanh()

    def parameters(self):
        return self.w + [self.b]
    
x = [2.0, 3.0]
n = Neuron(2)
n(x)

Value(label= data=-0.71630401051218)

class Layer:
    def __init__(self, nin, nout):
        self.neurons = [Neuron(nin
                              ) for _ in range(nout)]
    
    def __call__(self, x):
        outs = [n(x) for n in self.neurons]
        return outs[0] if len(outs) == 1 else outs
    
    def parameters(self):
        return [p for neuron in self.neurons for p in neuron.parameters()]

x = [2.0, 3.0]
n = Layer(2, 3)
n(x)

[
    Value(label= data=0.9323923071860208),
    Value(label= data=-0.6957480842688355),
    Value(label= data=0.9949508713128399)
]

class MLP:
    def __init__(self, nin, nouts):
        sz = [nin] + nouts
        self.layers = [Layer(sz[i], sz[i+1]) for i
                       in range(len(nouts))]
        
    def __call__(self, x):
        for layer in self.layers:
            x = layer(x)
        return x
    
    def parameters(self):
        return [p for layer in self.layers for p in layer.parameters()]

x = [2.0, 3.0, -1.0]
n = MLP(3, [4, 4, 1])
o = n(x)
o.grad = 1
o.backward()

n.parameters(), len(n.parameters())

(
    [
        Value(label= data=-0.8773320545613115),
        Value(label= data=0.21854271535158198),
        Value(label= data=0.13730892829595565),
        Value(label= data=-0.5436703421639371),
        Value(label= data=-0.5007041170945776),
        Value(label= data=0.9789830631658898),
        Value(label= data=0.8050974151663517),
        Value(label= data=-0.11016135996456167),
        Value(label= data=0.22124094253907778),
        Value(label= data=-0.8692488975746844),
        Value(label= data=-0.51512083826767),
        Value(label= data=-0.15884614255298235),
        Value(label= data=-0.9216734804692623),
        Value(label= data=0.6165197184222242),
        Value(label= data=0.33389808347375305),
        Value(label= data=0.6716163019747723),
        Value(label= data=0.7479127489965471),
        Value(label= data=0.6913996844396202),
        Value(label= data=-0.3719520946883914),
        Value(label= data=0.0381466491267759),
        Value(label= data=-0.8036261340897828),
        Value(label= data=0.14331062776761772),
        Value(label= data=-0.9904951973594573),
        Value(label= data=0.23265417282124412),
        Value(label= data=-0.5441204768729622),
        Value(label= data=0.09037344168895323),
        Value(label= data=-0.6263186959547287),
        Value(label= data=-0.7687145874568115),
        Value(label= data=0.8067183837857432),
        Value(label= data=-0.6695236110998573),
        Value(label= data=-0.4936725683149976),
        Value(label= data=-0.948783805686829),
        Value(label= data=-0.362064305878842),
        Value(label= data=0.71706547232376),
        Value(label= data=-0.38398098767491895),
        Value(label= data=-0.854407056637168),
        Value(label= data=-0.43771644655834585),
        Value(label= data=-0.8122254391243122),
        Value(label= data=-0.7849921896499341),
        Value(label= data=0.7867428242639574),
        Value(label= data=0.9508849142793219)
    ],
    41
)

draw_dot(o, label)

Tiny Dataset with loss function

xs = [
    [2.0, 3.0, -1.0],
    [3.0, -1.0, 0.5],
    [0.5, 1.0, 1.0], 
    [1.0, 1.0, -1.0]
]
ys = [1.0, -1.0, -1.0, 1.0]

ypred = [n(x) for x in xs]
loss = sum([(yout - ygt)**2 for ygt, yout in zip(ys, ypred)])
loss

Value(label= data=6.145450264034548)

ypred

[
    Value(label= data=0.9613622740038076),
    Value(label= data=0.5091506010451603),
    Value(label= data=0.9497390552324829),
    Value(label= data=0.7451677610062515)
]

Repeat

loss.backward()

n.layers[0].neurons[0].w[0].grad

-0.04473465638916681

n.layers[0].neurons[0].w[0].data

-0.8773320545613115

for p in n.parameters():
    p.data += -0.01 * p.grad

n.layers[0].neurons[0].w[0].data

-0.8768847079974198

ypred = [n(x) for x in xs]
loss = sum([(yout - ygt)**2 for ygt, yout in zip(ys, ypred)])
loss

Value(label= data=5.9448254035134465)

ypred

[
    Value(label= data=0.9617265322081271),
    Value(label= data=0.43565539138090165),
    Value(label= data=0.9510677256835314),
    Value(label= data=0.725065694807515)
]

n.parameters()

[
    Value(label= data=-0.8768847079974198),
    Value(label= data=0.21949508647796803),
    Value(label= data=0.1385938942733024),
    Value(label= data=-0.5427509639370535),
    Value(label= data=-0.4989987951971535),
    Value(label= data=0.9810637753982486),
    Value(label= data=0.8032841357361882),
    Value(label= data=-0.10822461638644491),
    Value(label= data=0.2191073445250642),
    Value(label= data=-0.8693341479297328),
    Value(label= data=-0.5150553447581354),
    Value(label= data=-0.1599712708867693),
    Value(label= data=-0.9204522149327646),
    Value(label= data=0.6176978033162941),
    Value(label= data=0.33248584468999454),
    Value(label= data=0.6728960760418363),
    Value(label= data=0.7467247012385713),
    Value(label= data=0.6928044491564865),
    Value(label= data=-0.3733392595509354),
    Value(label= data=0.03928302778692913),
    Value(label= data=-0.8017417247095591),
    Value(label= data=0.14178985429307983),
    Value(label= data=-0.9916730215251183),
    Value(label= data=0.23454886497577554),
    Value(label= data=-0.5461943160052498),
    Value(label= data=0.09193046790217876),
    Value(label= data=-0.6258347045651111),
    Value(label= data=-0.768590750645844),
    Value(label= data=0.8076512515956322),
    Value(label= data=-0.6702462673395139),
    Value(label= data=-0.49429632745656293),
    Value(label= data=-0.9460952730831453),
    Value(label= data=-0.3596651251112354),
    Value(label= data=0.7141165005167276),
    Value(label= data=-0.3806245013086102),
    Value(label= data=-0.8570897419717581),
    Value(label= data=-0.41643954968132757),
    Value(label= data=-0.8282591500009012),
    Value(label= data=-0.8021962015254895),
    Value(label= data=0.7707916705043153),
    Value(label= data=0.9262723943108128)
]

Make the above Repeat section into training loop

def train(repeats, model, xs, ygt, lr = 0.01):
    
    for k in range(repeats):
        # forward pass
        ypred = [model(x) for x in xs]
        loss = sum((yout - ygt)**2 for ygt, yout in zip(ygt, ypred))
        print(k, loss.data)
        
        # backward propagation
        for p in n.parameters(): p.grad = 0.0 # zero_grad()
        loss.backward()
        
        # update: gradient descent
        for p in model.parameters(): p.data += -lr * p.grad
    return ypred

xs = [
    [2.0, 3.0, -1.0],
    [3.0, -1.0, 0.5],
    [0.5, 1.0, 1.0], 
    [1.0, 1.0, -1.0]
]
ys = [1.0, -1.0, -1.0, 1.0]

model = MLP(3, [4, 4, 1])

train(10, model, xs, ys, 0.05)

0 7.220472885146723

1 6.8361918435934355

2 5.589046560434221

3 4.147937671605216

4 4.875203300452224

5 4.323610795464504

6 3.546174609092321

7 1.7412962395817813

8 0.5351626826196177

9 0.21335050879201323

[
    Value(label= data=0.5781623601547444),
    Value(label= data=-0.8870687314798208),
    Value(label= data=-0.8905626911927673),
    Value(label= data=0.896687278453952)
]

Done!